题目内容
如图,在底面是一直角梯形的四棱锥S—ABCD中,AD∥BC,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=
解析:本题是“无棱”的二面角,利用向量法求二面角大小更显示了向量工具的魅力.抓住AD、AB、AS两两互相垂直建立坐标系,用待定系数法求出面SAB、面SCD的法向量,再求其夹角.?
解:如图,建立空间直角坐标系,则A(0,0,0),B(0,1,0),C(1,1,0),D(![]() ,0,0),S(0,0,1),得
,0,0),S(0,0,1),得![]() =(
=(![]() ,1,0),
,1,0),![]() =(
=(![]() ,0,-1),
,0,-1),![]() =(1,1,-1).?
=(1,1,-1).?
设平面SDC的法向量为n1=(x1,y1,z1).?
∵n1⊥面SDC,∴n1⊥![]() ,n1⊥
,n1⊥![]() .?
.?
∴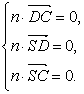 ∴
∴
∴
∴n1=(x1,-![]() x1,
x1,![]() x1).?
x1).?
设平面SAD的法向量为n2=(x2,y2,z2),则![]() =(0,0,-1),
=(0,0,-1),![]() =(0,1,-1),?
=(0,1,-1),?
∴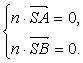
∴
∴z2=y2=0.∴n2=(x2,0,0).?
∴cos〈n1,n2〉=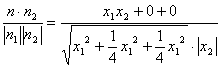
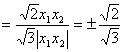 .?
.?
∵面SAB与面SCD所成角的二面角为锐角,为θ,?
∴cosθ=|cos〈n1,n2〉|=![]() .?
.?
∴θ=arccos![]() .?
.?
故面SCD与面SBA所成的角为arccos![]() .
.

练习册系列答案
相关题目
 (2012•宿州一模)如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.
(2012•宿州一模)如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.
