题目内容
若![]()
且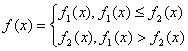
(1)求![]() 对所有实数
对所有实数![]() 成立的充要条件(用
成立的充要条件(用![]() 表示)
表示)
(2)设![]() 为两实数,
为两实数,![]() 且
且![]() 若
若![]()
求证:![]() 在区间
在区间![]() 上的单调增区间的长度和为
上的单调增区间的长度和为![]() (闭区间
(闭区间![]() 的长度定义为
的长度定义为![]() )
)
解:(Ⅰ)![]() 恒成立
恒成立![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (*)
(*)
因为![]()
所以,故只需![]()
![]() (*)恒成立
(*)恒成立
综上所述,![]() 对所有实数成立的充要条件是:
对所有实数成立的充要条件是:![]()
![]()
(Ⅱ)1°如果![]()
![]() ,则的图象关于直线
,则的图象关于直线![]() 对称.因为
对称.因为![]() ,所以区间
,所以区间![]() 关于直线
关于直线![]() 对称.
对称.
因为减区间为![]() ,增区间为
,增区间为![]() ,所以单调增区间的长度和为
,所以单调增区间的长度和为![]()
2°如果![]()
![]() .
.
(1)当![]()
![]() 时.
时. ,
,
当![]() ,
,![]() 因为
因为![]() ,所以
,所以![]() ,
,
故![]() =
=![]()
当![]() ,
,![]() 因为
因为![]() ,所以
,所以![]()
故![]() =
=![]()
因为![]() ,所以
,所以![]() ,所以
,所以![]() 即
即
![]()
当![]() 时,令
时,令![]() ,则
,则![]() ,所以
,所以![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() =
=![]()
![]() 时,
时,![]() ,所以
,所以![]() =
=![]()
![]() 在区间
在区间![]() 上的单调增区间的长度和
上的单调增区间的长度和![]()
=![]()
(2)当![]()
![]() 时.
时. ,
,
当![]() ,
,![]() 因为
因为![]() ,所以
,所以![]() ,
,
故![]() =
=![]()
当![]() ,
,![]() 因为
因为![]() ,所以
,所以![]()
故![]() =
=![]()
因为![]() ,所以
,所以![]() ,所以
,所以![]()
当![]() 时,令
时,令![]() ,则
,则![]() ,所以
,所以![]() ,
,
当![]() 时,
时, ![]() ,所以
,所以![]() =
=![]()
![]() 时,
时,![]() ,所以
,所以![]() =
=![]()
![]() 在区间
在区间![]() 上的单调增区间的长度和
上的单调增区间的长度和![]()
=![]()
综上得![]() 在区间
在区间![]() 上的单调增区间的长度和为
上的单调增区间的长度和为![]()

练习册系列答案
相关题目
 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=2a,AD=
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=2a,AD=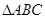 中,
中, 、
、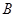 、
、 所对的边分别为
所对的边分别为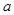 、
、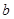 、
、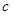 .已知向量
.已知向量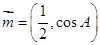 ,
, ,且
,且 .
.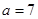 ,
,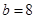 ,求
,求 的内角
的内角 所对边分别为
所对边分别为 ,且
,且 .
. 的大小;
的大小; ,求边长
,求边长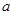 的最小值.
的最小值. 的三个内角A、B、C所对的边分别为
的三个内角A、B、C所对的边分别为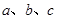 ,向量
,向量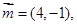
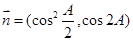 ,且
,且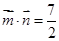 .
.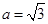 ,试判断
,试判断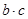 取得最大值时
取得最大值时 ,且
,且
 ,求
,求 的取值范围.
的取值范围.