题目内容
 (2013•湖南模拟)某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形,则该几何体的表面积为( )
(2013•湖南模拟)某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形,则该几何体的表面积为( )分析:根据题意,该几何体是一个四棱锥,其底面是边长分别为6和8的矩形,侧棱长均相等且高SO=4.因此利用线面垂直的性质结合勾股定理算出等腰△SAB和等腰△SCB的高长,从而算出四个侧面等腰三角形的面积,结合矩形ABCD的面积即可得到该几何体的全面积.
解答:解:根据题意,可得该几何体是底面边长分别为6和8的矩形,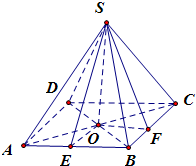
且侧棱长均相等的四棱锥,高长为SO=4,如图所示
因此,等腰△SAB的高SE=
=
=5
等腰△SCB的高SF=
=
=4
∴S△SAB=S△SCD=
×AB×SE=20,S△SCB=S△SAD=
×CB×SF=12
∵矩形ABCD的面积为6×8=48
∴该几何体的表面积为
S全=S△SAB+S△SCD+S△SCB+S△SAD+SABCD
=2×20+2×12
+48=24
+88
故选:B

且侧棱长均相等的四棱锥,高长为SO=4,如图所示
因此,等腰△SAB的高SE=
| SO2+OE2 |
| 42+32 |
等腰△SCB的高SF=
| SO2+OF2 |
| 42+42 |
| 2 |
∴S△SAB=S△SCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
∵矩形ABCD的面积为6×8=48
∴该几何体的表面积为
S全=S△SAB+S△SCD+S△SCB+S△SAD+SABCD
=2×20+2×12
| 2 |
| 2 |
故选:B
点评:本题给出四棱锥的三视图,要我们根据题中数据计算四棱锥的全面积,着重考查了线面垂直的性质、三视图的理解和锥体表面积计算等知识,属于基础题.

练习册系列答案
相关题目
 (2013•湖南模拟)设椭圆
(2013•湖南模拟)设椭圆 (2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=
(2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=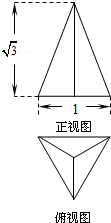 (2013•湖南模拟)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )
(2013•湖南模拟)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( ) (2013•湖南模拟)已知集合M={x∈Z|-1≤x≤1},N={x∈Z|x(x-2)≤0},则如图所示韦恩图中的阴影部分所表示的集合为( )
(2013•湖南模拟)已知集合M={x∈Z|-1≤x≤1},N={x∈Z|x(x-2)≤0},则如图所示韦恩图中的阴影部分所表示的集合为( )