题目内容
等差数列{an}中，已知a1=-12，S13=0，使得an＜0的最大正整数n为（ ）
| A．6 | B．7 | C．8 | D．9 |
设等差数列{an}的公差为d，
∵a1=-12，S13=0，∴0=
，
解得a13=12．
∴12=a13=a1+12d=-12+12d，解得d=2．
∴an=-12+2（n-1）=2n-14，
令an=0，解得n=7．
∴使得an＜0的最大正整数n=6．
故选：A．
∵a1=-12，S13=0，∴0=
| 13(-12+a13) |
| 2 |
解得a13=12．
∴12=a13=a1+12d=-12+12d，解得d=2．
∴an=-12+2（n-1）=2n-14，
令an=0，解得n=7．
∴使得an＜0的最大正整数n=6．
故选：A．
练习册系列答案
轻松暑假总复习系列答案
相关题目
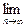(d1+d2+…+dn)的值是( )