题目内容
某工厂在1999年的“减员增效”中对部分人员实行分流,规定分流人员第一年可以到原单位领取工资的100%,从第二年起,以后每年只能在原单位按上一年的
领取工资,该厂根据分流人员的技术特长,计划创办新的经济实体,该经济实体预计第一年属投资阶段,第二年每人可获得b元收入,从第三年起每人每年的收入可在上一年的基础上递增50%,如果某人分流前工资的收入每年a元,分流后进入新经济实体,第n年的收入为an元,
(1)求{an}的通项公式;
(2)当b=
时,这个人哪一年的收入最少?最少为多少?
(3)当b≥
时,是否一定可以保证这个人分流一年后的收入永远超过分流前的年收入?
| 2 |
| 3 |
(1)求{an}的通项公式;
(2)当b=
| 8a |
| 27 |
(3)当b≥
| 3a |
| 8 |
分析:(1)由题意知职工分流后每年的工资组成一个数列,由两个等比数列的和组成,代入数据求{an}的通项公式.
(2)把b的值代入通项公式an,再利用基本不等式求最小值.
(3)根据(1)求出的an和b的范围,放缩一次后,再利用基本不等式进行比较,注意等号成立的条件,再回到实际问题中.
(2)把b的值代入通项公式an,再利用基本不等式求最小值.
(3)根据(1)求出的an和b的范围,放缩一次后,再利用基本不等式进行比较,注意等号成立的条件,再回到实际问题中.
解答:解:(1)由题意得,当n=1时,a1=a,
当n≥2时,an=a(
)n-1+b(
)n-2,
∴an=
.
(2) 由已知b=
,
当n≥2时,an=a(
)n-1+
(
)n-2≥2[a(
)n-1×
(
)n-2]
=
要使得上式等号成立,当且仅当a(
)n-1=
(
)n-2,
即(
)2n-2=(
)4,解得n=3,
因此这个人第三年收入最少为
元.
(3)∵当n≥2时,an=a(
)n-1+b(
)n-2≥a(
)n-1+
(
)n-2≥2
=a,
上述等号成立时,须b=
且a(
)n-1=
(
)n-2,即(
)n-1=
两边取对数得,n=1+log
>1+log
=2,因此等号不能取到,
∴当b≥
时,这个人分流一年后的收入永远超过分流前的年收入.
当n≥2时,an=a(
| 2 |
| 3 |
| 3 |
| 2 |
∴an=
|
(2) 由已知b=
| 8a |
| 27 |
当n≥2时,an=a(
| 2 |
| 3 |
| 8a |
| 27 |
| 3 |
| 2 |
| 2 |
| 3 |
| 8a |
| 27 |
| 3 |
| 2 |
| 1 |
| 2 |
| 8a |
| 9 |
要使得上式等号成立,当且仅当a(
| 2 |
| 3 |
| 8a |
| 27 |
| 3 |
| 2 |
即(
| 2 |
| 3 |
| 2 |
| 3 |
因此这个人第三年收入最少为
| 8a |
| 9 |
(3)∵当n≥2时,an=a(
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
| 3a |
| 8 |
| 3 |
| 2 |
a(
|
上述等号成立时,须b=
| 3a |
| 8 |
| 2 |
| 3 |
| 3a |
| 8 |
| 3 |
| 2 |
| 4 |
| 9 |
| 1 |
| 4 |
两边取对数得,n=1+log
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
∴当b≥
| 3a |
| 8 |
点评:本题为等比数列应用题,通项公式只能用分段函数表示,不能合二为一;在求最值和比较大小时,用到了基本不等式,注意等号成立时是否取到.

练习册系列答案
相关题目
 领取工资,该厂根据分流人员的技术特长,计划创办新的经济实体,该经济实体预计第一年属投资阶段,第二年每人可获得b元收入,从第三年起每人每年的收入可在上一年的基础上递增50%,如果某人分流前工资的收入每年a元,分流后进入新经济实体,第n年的收入为an元,
领取工资,该厂根据分流人员的技术特长,计划创办新的经济实体,该经济实体预计第一年属投资阶段,第二年每人可获得b元收入,从第三年起每人每年的收入可在上一年的基础上递增50%,如果某人分流前工资的收入每年a元,分流后进入新经济实体,第n年的收入为an元,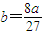 时,这个人哪一年的收入最少?最少为多少?
时,这个人哪一年的收入最少?最少为多少?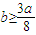 时,是否一定可以保证这个人分流一年后的收入永远超过分流前的年收入?
时,是否一定可以保证这个人分流一年后的收入永远超过分流前的年收入?