题目内容
已知公比为q(0<q<1)的无穷等比数列{an}各项的和为9,无穷等比数列{an2}各项的和为
.
(1)求数列{an}的首项a1和公比q;
(2)对给定的k(k=1,2,3,…,n),设T(k)是首项为ak,公差为2ak-1的等差数列,求T(2)的前2007项之和;
(3)(理)设bi为数列T(i)的第i项,Sn=b1+b2+…+bn:
①求Sn的表达式,并求出Sn取最大值时n的值.
②求正整数m(m>1),使得
存在且不等于零.
(文)设bi为数列T(i)的第i项,Sn=b1+b2+…+bn:求Sn的表达式,并求正整数m(m>1),使得
存在且不等于零.
| 81 |
| 5 |
(1)求数列{an}的首项a1和公比q;
(2)对给定的k(k=1,2,3,…,n),设T(k)是首项为ak,公差为2ak-1的等差数列,求T(2)的前2007项之和;
(3)(理)设bi为数列T(i)的第i项,Sn=b1+b2+…+bn:
①求Sn的表达式,并求出Sn取最大值时n的值.
②求正整数m(m>1),使得
| lim |
| n→∞ |
| Sn |
| nm |
(文)设bi为数列T(i)的第i项,Sn=b1+b2+…+bn:求Sn的表达式,并求正整数m(m>1),使得
| lim |
| n→∞ |
| Sn |
| nm |
(1)依题意可知,
?
.
(2)由(1)知,an=3×(
)n-1,所以数列T(2)的首项为t1=a2=2,公差d=2a2-1=3,S2007=2007×2+
×2007×2006×3=6043077,即数列的前2007项之和为6043077.
(3)(理)bi=ai+(i-1)(2ai-1)=(2i-1)ai-(i-1)=3(2i-1)(
)i-1-(i-1);
①Sn=45-(18n+27)(
)n-
;
由
,解得n=2,
计算可得b1=3,b2=5,b3=
,b4=
,b5=
,b6=-
<0,
因为当n≥2时,bn>bn+1,所以Sn当n=5时取最大值.
②
=
-
(
)n-
,
当m=2时,
=-
,当m>2时,
=0,所以m=2.
(文)bi=ai+(i-1)(2ai-1)=(2i-1)ai-(i-1)=3(2i-1)(
)i-1-(i-1);Sn=45-(18n+27)(
)n-
;
=
-
(
)n-
,
当m=2时,
=-
,当m>2时,
=0,所以m=2.
|
|
(2)由(1)知,an=3×(
| 2 |
| 3 |
| 1 |
| 2 |
(3)(理)bi=ai+(i-1)(2ai-1)=(2i-1)ai-(i-1)=3(2i-1)(
| 2 |
| 3 |
①Sn=45-(18n+27)(
| 2 |
| 3 |
| n(n-1) |
| 2 |
由
|
计算可得b1=3,b2=5,b3=
| 14 |
| 3 |
| 29 |
| 9 |
| 4 |
| 3 |
| 53 |
| 81 |
因为当n≥2时,bn>bn+1,所以Sn当n=5时取最大值.
②
| lim |
| n→∞ |
| Sn |
| nm |
| lim |
| n→∞ |
| 45 |
| nm |
| 18n+27 |
| nm |
| 2 |
| 3 |
| n(n-1) |
| 2nm |
当m=2时,
| lim |
| n→∞ |
| Sn |
| nm |
| 1 |
| 2 |
| lim |
| n→∞ |
| Sn |
| nm |
(文)bi=ai+(i-1)(2ai-1)=(2i-1)ai-(i-1)=3(2i-1)(
| 2 |
| 3 |
| 2 |
| 3 |
| n(n-1) |
| 2 |
| lim |
| n→∞ |
| Sn |
| nm |
| lim |
| n→∞ |
| 45 |
| nm |
| 18n+27 |
| nm |
| 2 |
| 3 |
| n(n-1) |
| 2nm |
当m=2时,
| lim |
| n→∞ |
| Sn |
| nm |
| 1 |
| 2 |
| lim |
| n→∞ |
| Sn |
| nm |

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
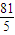 .
.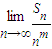 存在且不等于零.
存在且不等于零.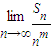 存在且不等于零.
存在且不等于零.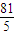 .
.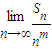 存在且不等于零.
存在且不等于零.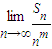 存在且不等于零.
存在且不等于零.