题目内容
已知函数f（x）=x2+2cosx，则关于x的方程
的所有实根之和为
- A.0
- B.-2
- C.-4
- D.-6
C
分析：求导函数，确定函数的单调性，从而脱去函数符号，利用韦达定理，即可求得结论．
解答：求导函数可得：f′（x）=2x-2sinx
当x≥0时，f′（x）≥0，∴f（x）在[0，+∞）上递增
∵f（-x）=f（x），∴函数为偶函数，
∴方程等价于
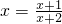或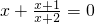
∴x2+x-1=0或x2+3x+1=0
∴方程所有实根之和为-4
故选C．
点评：本题考查导数知识的运用，考查函数的单调性，解题的关键是转化为具体方程，属于中档题．
分析：求导函数，确定函数的单调性，从而脱去函数符号，利用韦达定理，即可求得结论．
解答：求导函数可得：f′（x）=2x-2sinx
当x≥0时，f′（x）≥0，∴f（x）在[0，+∞）上递增
∵f（-x）=f（x），∴函数为偶函数，
∴方程
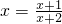等价于或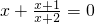∴x2+x-1=0或x2+3x+1=0
∴方程所有实根之和为-4
故选C．
点评：本题考查导数知识的运用，考查函数的单调性，解题的关键是转化为具体方程，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|