题目内容
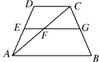如图，在等腰梯形中，AB∥CD，AD=12 cm，AC交梯形中位线EG于点F，EF=4cm，FG=10cm．求此梯形的面积．
分析：做出辅助线，过上底的顶点向下底做高，根据梯形的中位线得到F是中点，得到要用的长度值，可以证明两个三角形相似，得到AM的长，根据勾股定理求出要的结果．
解答：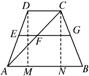
解：如图所示，作高DM、CN，则四边形DMNC为矩形．
∵EG是梯形ABCD的中位线，
∴EG∥DC∥AB．
∴F是AC的中点．
∴DC=2EF=8，AB=2FG=20，MN=DC=8．
在Rt△ADM和Rt△BCN中，
AD=BC，∠DAM=∠CBN，∠AMD=∠BNC=90°，
∴△ADM≌△BCN．
∴AM=BN=
（20-8）=6，
∴DM=
=
=6
，
∴S梯形=EG•DM=14×6
=84
（cm2）．
解：如图所示，作高DM、CN，则四边形DMNC为矩形．∵EG是梯形ABCD的中位线，
∴EG∥DC∥AB．
∴F是AC的中点．
∴DC=2EF=8，AB=2FG=20，MN=DC=8．
在Rt△ADM和Rt△BCN中，
AD=BC，∠DAM=∠CBN，∠AMD=∠BNC=90°，
∴△ADM≌△BCN．
∴AM=BN=
| 1 |
| 2 |
∴DM=
| AD2-AM2 |
| 122-62 |
| 3 |
∴S梯形=EG•DM=14×6
| 3 |
| 3 |
点评：本题考查平行线等分线段定理，考查两个三角形全等，考查勾股定理，是一个结合计算和证明于一体的平面几何题目，考查的比较全面，是一个综合题目．
练习册系列答案
相关题目
中，已知
均为梯形的高，且
。现沿
将
和
折起，使点
重合为一点
，如图②所示。又点
为线段
的中点，点
在线段
上，且
。
的长；
的大小。
中，
，过点
作
的平行线
，交
的延长线于点
.求证：⑴ 
⑵ 
中，
，且
. 设
，
，以
，
为焦点且过点
的双曲线的离心率为
，以
，
，则( )
的增大，
为定值
中，
，且
.设
，以
为焦点且过点
的双曲线的离心率为
，以
为焦点且过点
的椭圆的离心率为
，则
（ ）
的增大，
为定值