题目内容
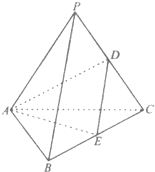 (2013•汕头一模)在三棱锥P-ABC中.侧梭长均为4.底边AC=4.AB=2,BC=2
(2013•汕头一模)在三棱锥P-ABC中.侧梭长均为4.底边AC=4.AB=2,BC=2| 3 |
〔I)求证:平面PAC⊥平面ABC.
(Ⅱ)求三棱锥P-ABC的体积;
(Ⅲ)求二面角C-AD-E的余弦值.
分析:(I)利用等腰三角形的性质即可得到OP⊥AC,再利用勾股定理的逆定理即可得到OP⊥OB,利用线面垂直的判定定理即可证明;
(II)由(I)可知OP⊥平面ABC,故OP为三棱锥P-ABC的高,且OP=2
,直角三角形ABC的面积S=
AB×BC,再利用VP-ABC=
S△ABC×OP即可得出.
(III)方法一:过点E 作EH⊥AC于H,过点H作HM⊥AD于M,连接ME,由平面PAC⊥平面ABC,EH⊥AC,EH?平面ABC,可得EH⊥平面PAC,于是ME⊥AD(三垂线定理),可得∠EMH即为所求的二面角的平面角.利用直角三角形的边角关系求出即可.
方法二:以O为原点,建立如图所示的空间直角坐标系,利用两个平面的法向量即可得到二面角.
(II)由(I)可知OP⊥平面ABC,故OP为三棱锥P-ABC的高,且OP=2
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
(III)方法一:过点E 作EH⊥AC于H,过点H作HM⊥AD于M,连接ME,由平面PAC⊥平面ABC,EH⊥AC,EH?平面ABC,可得EH⊥平面PAC,于是ME⊥AD(三垂线定理),可得∠EMH即为所求的二面角的平面角.利用直角三角形的边角关系求出即可.
方法二:以O为原点,建立如图所示的空间直角坐标系,利用两个平面的法向量即可得到二面角.
解答: 证明:(Ⅰ)∵PA=PB=PC=AC=4,
证明:(Ⅰ)∵PA=PB=PC=AC=4,
取AC的中点O,连接OP,OB,可得:OP⊥AC,
OP=
=
=2
,
∵AC=4,AB=2,BC=2
,∴AC2=AB2+BC2,∴△ABC为Rt△.
∴OB=OC=2,PB2=OB2+OP2,∴OP⊥OB.
又∵AC∩BO=O且AC、OB?面ABC,∴OP⊥平面ABC,
又∵OP?平面PAC,∴平面PAC⊥平面ABC.)
(Ⅱ)由(I)可知:OP⊥平面ABC,∴OP为三棱锥P-ABC的高,且OP=2
.
直角三角形ABC的面积S=
AB×BC=
×2×2
=2
.
∴VP-ABC=
S△ABC×OP=
×2
×2
=4.
(Ⅲ)方法一:过点E 作EH⊥AC于H,过点H作HM⊥AD于M,
连接ME,∵平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,EH⊥AC,EH?平面ABC,
∴EH⊥平面PAC,∴ME⊥AD(三垂线定理),
∴∠EMH即为所求的二面角的平面角.
∵E,D分别为中点,EH⊥AC,
∴在RT△HEC中:HC=ECcos300=
,EH=ECsin300=
,
∴AH=4-HC=
在RT△HMA中,MH=AHsin300=
.
在RT△HME中,ME=
=
=
.
所以cos∠EMH=
=
=
.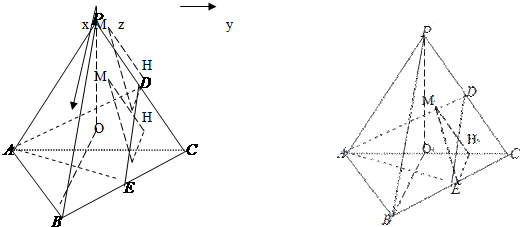
方法二:以O为原点,建立如图所示的空间直角坐标系,
O(0,0,0),A(0,-2,0),B(
,-1,0),C(0,2,0),D(0,1,
),E(
,
,0),P(0,0,2
),
∴
=(
,
,0),
=(0,3,
),
设平面AED的一个法向量为
1=(x,y,z),
平面ACD的一个法向量为
2=(1,0,0),
则
,得
,令x=1,则y=-
,z=
.
∴
=(1,-
,
),
设所求的二面角为θ,显然θ为锐角,
cosθ=|cos<
,
>|=
=
=
.
 证明:(Ⅰ)∵PA=PB=PC=AC=4,
证明:(Ⅰ)∵PA=PB=PC=AC=4,取AC的中点O,连接OP,OB,可得:OP⊥AC,
OP=
| PC2-OC2 |
| 42-22 |
| 3 |
∵AC=4,AB=2,BC=2
| 3 |
∴OB=OC=2,PB2=OB2+OP2,∴OP⊥OB.
又∵AC∩BO=O且AC、OB?面ABC,∴OP⊥平面ABC,
又∵OP?平面PAC,∴平面PAC⊥平面ABC.)
(Ⅱ)由(I)可知:OP⊥平面ABC,∴OP为三棱锥P-ABC的高,且OP=2
| 3 |
直角三角形ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴VP-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
(Ⅲ)方法一:过点E 作EH⊥AC于H,过点H作HM⊥AD于M,
连接ME,∵平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,EH⊥AC,EH?平面ABC,
∴EH⊥平面PAC,∴ME⊥AD(三垂线定理),
∴∠EMH即为所求的二面角的平面角.
∵E,D分别为中点,EH⊥AC,
∴在RT△HEC中:HC=ECcos300=
| 3 |
| 2 |
| ||
| 2 |
∴AH=4-HC=
| 5 |
| 2 |
在RT△HMA中,MH=AHsin300=
| 5 |
| 4 |
在RT△HME中,ME=
| HE2+HM2 |
|
| ||
| 4 |
所以cos∠EMH=
| MH |
| ME |
| ||||
|
5
| ||
| 37 |

方法二:以O为原点,建立如图所示的空间直角坐标系,
O(0,0,0),A(0,-2,0),B(
| 3 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
∴
| AE |
| ||
| 2 |
| 5 |
| 2 |
| AD |
| 3 |
设平面AED的一个法向量为
| n |
平面ACD的一个法向量为
| n |
则
|
|
| ||
| 5 |
| 3 |
| 5 |
∴
| n1 |
| ||
| 5 |
| 3 |
| 5 |
设所求的二面角为θ,显然θ为锐角,
cosθ=|cos<
| n1 |
| n2 |
|
| ||||
|
|
| 1 | ||||||
|
5
| ||
| 37 |
点评:熟练掌握等腰三角形的性质、勾股定理的逆定理、线面垂直的判定和性质定理、三棱锥的体积计算公式、利用三垂线定理和二面角的定义求得二面角的平面角、通过空间直角坐标系利用两个平面的法向量得到二面角等是解题的关键.

练习册系列答案
相关题目