题目内容
已知函数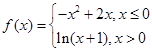
，若|f(x)|≥ax，则a的取值范围是（ ）
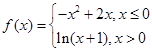，若|f(x)|≥ax，则a的取值范围是（ ）| A．(－∞，0] | B．(－∞，1] |
| C．[－2,1] | D．[－2,0] |
D
函数y＝|f(x)|的图象如图．
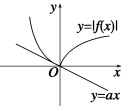
①当a＝0时，|f(x)|≥ax显然成立．
②当a>0时，只需在x>0时，
ln(x＋1)≥ax成立．
比较对数函数与一次函数y＝ax的增长速度．
显然不存在a>0使ln(x＋1)≥ax在x>0上恒成立．
③当a<0时，只需在x<0时，x2－2x≥ax成立．
即a≥x－2成立，∴a≥－2.
综上所述：－2≤a≤0.故选D.
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
的图象如右图所示，则下列函数正确的是 （ ）
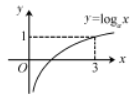
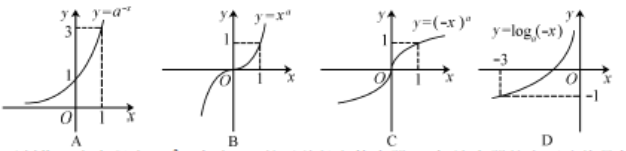
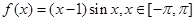的图象为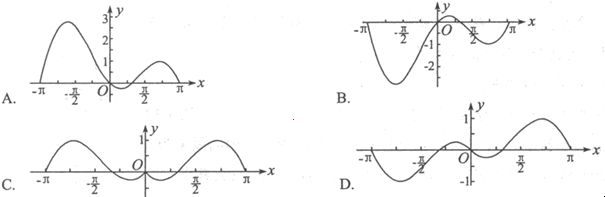
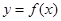是周期为2的周期函数，且当
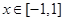时，
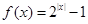，则函数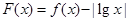
的零点个数是（ ）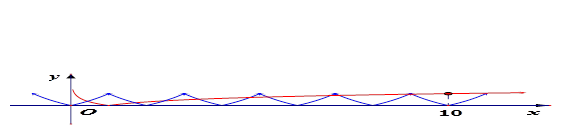
的图象如图所示，在区间
上可找到
个不同的数
，使得
，则n的取值范围是( )
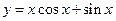的图象大致为( )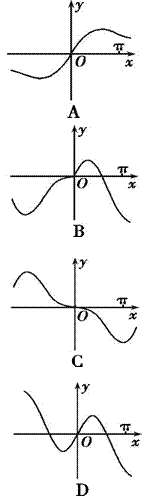
于E，当
从左至右移动（与线段AB有公共点）时，把四边形ABCD分成两部分，设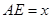
，左侧部分面积为
，则
的图像大致为( )
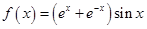的部分图象大致为（ ）