题目内容
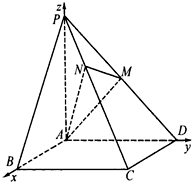
如图，已知四棱锥
的底面是正方形，
⊥底面
，且
，点
、
分别在侧棱
、
上，且
（Ⅰ）求证：
⊥平面
；
（Ⅱ）若
，求平面
与平面
的所成锐二面角的大小
（Ⅰ）见解析
（Ⅱ）平面AMN与PAB所成锐二面角的大小为
解析:
（Ⅰ）因为四棱锥P—ABCD的底面是正方形，PA⊥底面ABCD，
则CD⊥侧面PAD
又
又
……………5分
（Ⅱ）建立如图所示的空间直角坐标系
又PA=AD=2，
则有P（0，0，2），D（0，2，0）
|
设
则有
同理可得
即得
…………………………8分
由
而平面PAB的法向量可为
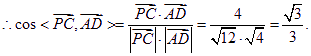
故所求平面AMN与PAB所成锐二面角的大小为
练习册系列答案
暑假作业海燕出版社系列答案
相关题目
（本题满分12分） 如图：已知四棱锥
的底面是平行四边形，
,垂足
在边
上，△
是等腰直角三角形，
,四面体
的体积为
．
与底面
所成的锐二面角的大小；
到面
在直线
上，且
,求
的值．
的底面是正方形，
，且
，点
分别在侧棱
、
上，且
。
；
，求平面
与平面
所成二面角的余弦值．
的底面是正方形，
⊥底面
，且
，点
、
分别为侧棱
、
的中点 
∥平面
；
⊥平面
.
的底面为矩形，
且
平面
分别为
的中点.
；
的大小值.