题目内容
将面积为2的长方形ABCD沿对角线AC折起,使二面角D-AC-B的大小为α(0°<α<180°),则三棱锥D-ABC的外接球的体积的最小值是
- A.
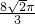
- B.
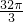
- C.

- D.与α的值有关的数
C
分析:由题意可知,AC的中点就是外接球的球心,三棱锥D-ABC的外接球的体积的最小,就是球的半径最小,就是AC最短,利用长方形的面积求出AC的最小值即可.
解答:将面积为2的长方形ABCD沿对角线AC折起,使二面角D-AC-B的大小为α(0°<α<180°),则三棱锥D-ABC的外接球的球心就是AC 的中点,三棱锥D-ABC的外接球的体积的最小,就是球的半径最小,就是AC最短,由题意可设长方形的长为:a,宽为:b,所以ab=2,AC= ≥
≥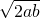 =2,此时a=b=
=2,此时a=b= ,AC=2,球的半径为:1,
,AC=2,球的半径为:1,
三棱锥D-ABC的外接球的体积的最小值是: .
.
故选C
点评:本题是基础题,考查球的内接多面体,确定体积的求法,本题的关键是确定球心,基本不等式的应用,考查转化思想,计算能力.
分析:由题意可知,AC的中点就是外接球的球心,三棱锥D-ABC的外接球的体积的最小,就是球的半径最小,就是AC最短,利用长方形的面积求出AC的最小值即可.
解答:将面积为2的长方形ABCD沿对角线AC折起,使二面角D-AC-B的大小为α(0°<α<180°),则三棱锥D-ABC的外接球的球心就是AC 的中点,三棱锥D-ABC的外接球的体积的最小,就是球的半径最小,就是AC最短,由题意可设长方形的长为:a,宽为:b,所以ab=2,AC=
 ≥
≥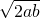 =2,此时a=b=
=2,此时a=b= ,AC=2,球的半径为:1,
,AC=2,球的半径为:1,三棱锥D-ABC的外接球的体积的最小值是:
 .
.故选C
点评:本题是基础题,考查球的内接多面体,确定体积的求法,本题的关键是确定球心,基本不等式的应用,考查转化思想,计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将面积为2的长方形ABCD沿对角线AC折起,使二面角D-AC-B的大小为α(0°<α<180°),则三棱锥D-ABC的外接球的体积的最小值是( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、与α的值有关的数 |








