题目内容
在 中,角
中,角 所对的边分别为
所对的边分别为 ,函数
,函数 在
在 处取得最大值.
处取得最大值.
(1)求角A的大小.
(2)若 且
且 ,求
,求 的面积.
的面积.
(1)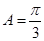 ;(2)
;(2) .
.
解析试题分析:(1)求角A的大小,由函数 ,对函数
,对函数 进行恒等变形,把函数
进行恒等变形,把函数 化为一个角的一个三角函数,即
化为一个角的一个三角函数,即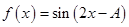 ,利用在
,利用在 处取得最大值,把
处取得最大值,把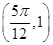 代入
代入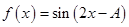 ,利用
,利用 ,即可求出角A的值;(2)若
,即可求出角A的值;(2)若 且
且 ,求
,求 的面积,由(1)知
的面积,由(1)知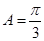 ,可考虑利用
,可考虑利用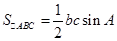 来求,因此只需求出
来求,因此只需求出 的值即可,由
的值即可,由 且
且 ,可利用正弦定理
,可利用正弦定理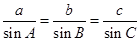 得
得 ,求出
,求出 的值,再利用余弦定理
的值,再利用余弦定理 可求出
可求出 的值,从而可得
的值,从而可得 的面积.
的面积.
试题解析:(1)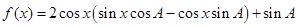
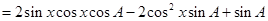
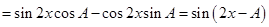 4分
4分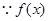 在
在 处取得最大值,
处取得最大值, 其中
其中 ,即
,即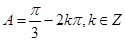
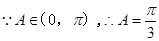 6分
6分
(2)由正弦定理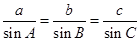 得
得 8分
8分
即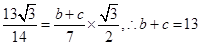 ,由余弦定理
,由余弦定理 得
得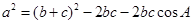 ,即
,即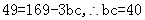
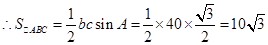 12分
12分
考点:三角恒等变化,解三角形.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 到
到 ,方位角(从正北方向顺时针转到
,方位角(从正北方向顺时针转到 方向所成的角)是
方向所成的角)是 ,距离是3km;从
,距离是3km;从 ,方位角是110°,距离是3km;从
,方位角是110°,距离是3km;从 ,方位角是140°,距离是(
,方位角是140°,距离是( )km.试画出大致示意图,并计算出从A到D的方位角和距离(结果保留根号).
)km.试画出大致示意图,并计算出从A到D的方位角和距离(结果保留根号). .
. 的最大值及最小正周期;
的最大值及最小正周期; ,
, ,求
,求 的值.
的值.
 ,△ABC的面积为
,△ABC的面积为 ,求
,求 .
. 、
、 、
、 为正实数,
为正实数, .
. 的三边长,且
的三边长,且 、
、 、
、 .若
.若 ,且
,且 .求
.求 .试证明长为
.试证明长为 .
. 中,角
中,角 的对边分别为
的对边分别为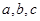 ,且
,且 又
又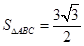 .
. 的大小;
的大小;  的值.
的值. 中,
中, ,
,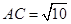 ,
,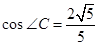 点
点 是
是 的中点, 求
的中点, 求
 的值和中线
的值和中线 的长
的长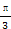 <C<
<C< 且
且 =
= .
. +
+ |=2,求
|=2,求 km的C、D两点,并且测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,求A、B之间的距离.
km的C、D两点,并且测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,求A、B之间的距离.