题目内容
已知1>n>m>0,则指数函数①y=mx,②y=nx的图象为( )
分析:利用指数函数底数a的大小与单调性的关系去判断.
解答:解:由1>n>m>0可知①②应为两条递减指数函数曲线,故只可能是选项C或D,
进而再判断①②与n和m的对应关系,
不妨选择特殊点,令x=1,则①②对应的函数值分别为m和n,
由m<n知选C.
故选:C.
进而再判断①②与n和m的对应关系,
不妨选择特殊点,令x=1,则①②对应的函数值分别为m和n,
由m<n知选C.
故选:C.
点评:本题考查指数函数的图象和性质,重点考查函数的单调性与底数a的对应关系.a>1,指数函数递增,0<a<1,指数函数递减.

练习册系列答案
相关题目
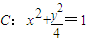 ,过点M(0,3)的直线l与椭圆C相交于不同的两点A、B.
,过点M(0,3)的直线l与椭圆C相交于不同的两点A、B.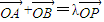 (O为坐标原点),求当|AB|<
(O为坐标原点),求当|AB|<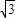 时,实数λ的取值范围.
时,实数λ的取值范围. ,过点M(0,3)的直线l与椭圆C相交于不同的两点A、B.
,过点M(0,3)的直线l与椭圆C相交于不同的两点A、B. (O为坐标原点),求当|AB|<
(O为坐标原点),求当|AB|< 时,实数λ的取值范围.
时,实数λ的取值范围.