题目内容
.已知函数![]() 同时满足:①不等式
同时满足:①不等式![]() 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在![]() ,使得不等式
,使得不等式![]() 成立.设数列
成立.设数列![]() 的前
的前![]() 项和为
项和为![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)设各项均不为零的数列![]() 中,所有满足
中,所有满足![]() 的正整数
的正整数![]() 的个数称为这个数列
的个数称为这个数列![]() 的变号数,令
的变号数,令![]() (
(![]() 为正整数),求数列
为正整数),求数列![]() 的变号数
的变号数
解:(1)由![]()
![]() 的解集有且只有一个元素知
的解集有且只有一个元素知
![]() 或
或![]() …………………………4分
…………………………4分
当![]() 时,函数
时,函数![]() 在
在![]() 上递增,此时不满足条件
上递增,此时不满足条件![]() ………………6分
………………6分
综上可知![]()
![]() …………………………8分
…………………………8分
(2)由条件可知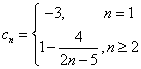
当![]() 时,令
时,令![]() 或
或![]()
所以![]() 或
或![]() ………………………………13分
………………………………13分
又![]() 时,也有
时,也有![]() ………………………………15分
………………………………15分
综上可得数列![]() 的变号数为3…
的变号数为3…

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
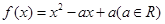 同时满足:①不等式
同时满足:①不等式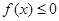 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在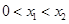 ,使得不等式
,使得不等式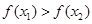 成立 设数列
成立 设数列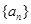 的前
的前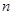 项和为
项和为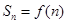
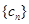 中,所有满足
中,所有满足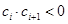 的正整数
的正整数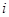 的个数称为这个数列
的个数称为这个数列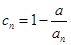 (
( 同时满足如下三个条件:①定义域为
同时满足如下三个条件:①定义域为 ;②
;② 时,
时, ,其中
,其中 .
. 上的解析式,并求出函数
上的解析式,并求出函数 ,
, 时,函数
时,函数 ,若
,若 的图象恒在直线
的图象恒在直线 上方,求实数
上方,求实数 的取值范围(其中
的取值范围(其中 为自然对数的底数,
为自然对数的底数, ).
). 若满足地f(a)=f(b)=f(c),(a、b、c互不相等),则a+b+c的取值范围是 .
若满足地f(a)=f(b)=f(c),(a、b、c互不相等),则a+b+c的取值范围是 . ,
, ,动点P(x,y)同时满足
,动点P(x,y)同时满足 则z=x+y的最大值是 .
则z=x+y的最大值是 .