题目内容
设a、b、c依次是△ABC的角A、B、C所对的边,若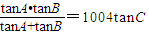 ,且a2+b2=mc2,则m= .
,且a2+b2=mc2,则m= .
【答案】分析:角三角函数的基本关系,正弦定理可得 c2=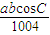 ,再根据 a2+b2=mc2,m=
,再根据 a2+b2=mc2,m=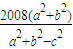 ,把余弦定理代入
,把余弦定理代入
可得m=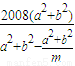 ,解方程求出m值.
,解方程求出m值.
解答:解:△ABC中,∵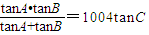 ,∴
,∴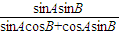 =1004
=1004 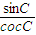 ,
,
∴sinAsinBcosC=1004sinC•sin(A+B)=1004sin2C,由正弦定理得
abcosC=1004c2,c2=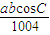 .
.
又∵a2+b2=mc2,∴a2+b2=m•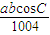 =
=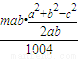 =
=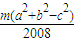 ,
,
∴m=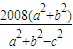 =
=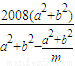 ,∴2008(a2+b2)=m(a2+b2)-( a2+b2 ).
,∴2008(a2+b2)=m(a2+b2)-( a2+b2 ).
∴m=2009,
故答案为:2009.
点评:本题考查同角三角函数的基本关系,正弦定理、余弦定理的应用,式子变形是解题的关键和难点.
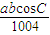 ,再根据 a2+b2=mc2,m=
,再根据 a2+b2=mc2,m=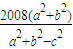 ,把余弦定理代入
,把余弦定理代入可得m=
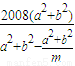 ,解方程求出m值.
,解方程求出m值.解答:解:△ABC中,∵
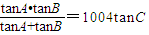 ,∴
,∴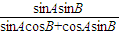 =1004
=1004 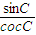 ,
,∴sinAsinBcosC=1004sinC•sin(A+B)=1004sin2C,由正弦定理得
abcosC=1004c2,c2=
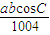 .
. 又∵a2+b2=mc2,∴a2+b2=m•
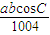 =
=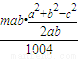 =
=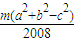 ,
,∴m=
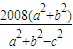 =
=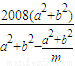 ,∴2008(a2+b2)=m(a2+b2)-( a2+b2 ).
,∴2008(a2+b2)=m(a2+b2)-( a2+b2 ).∴m=2009,
故答案为:2009.
点评:本题考查同角三角函数的基本关系,正弦定理、余弦定理的应用,式子变形是解题的关键和难点.

练习册系列答案
相关题目
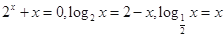 的根,则( )
的根,则( ) B.
B.  C.
C.
 D.
D.

 x=x的根,则( )
x=x的根,则( )