题目内容
若等腰直角三角形的直角边长为3，则以一直角边所在的直线为轴旋转一周所成的几何体体积是（ ）
分析：根据题意，旋转成的几何体为高与底面半径都等于3的圆锥，利用圆锥的体积公式即可算出该几何体的体积．
解答：解：∵等腰直角三角形的直角边长为3，
∴以等腰直角三角形的一直角边所在的直线为轴旋转一周，
所得的几何体是高与底面半径都等于3的圆锥，
因此，几何体的体积为V=
πr2h=
π×32×3=9π
故选：A
∴以等腰直角三角形的一直角边所在的直线为轴旋转一周，
所得的几何体是高与底面半径都等于3的圆锥，
因此，几何体的体积为V=
| 1 |
| 3 |
| 1 |
| 3 |
故选：A
点评：本题给出等腰直角三角形，求以它的一直角边所在的直线为轴旋转一周所成的几何体体积．着重考查了等腰直角三角形的性质、圆锥的形成过程和锥体体积公式等知识，属于基础题．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
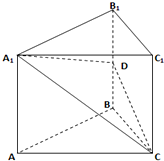如图，在直三棱柱ABC-A1B1C1中，底面△ABC为等腰直角三角形，∠B=90°，D为棱BB1上一点，且平面DA1C⊥平面AA1C1C．
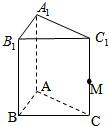直三棱柱ABC-A1B1C1中，底面ABC为等腰直角三角形，且AB⊥AC，AB=AC=2，AA1=4，M是侧棱CC1上一点，设MC=h．
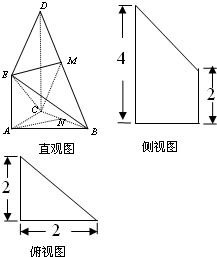（2012•烟台三模）如图是某直三棱柱（侧棱与底面垂直）被削去上底后的直观图与三视图的侧视图、俯视图，在直观图中，M是BD的中点，侧视图是直角梯形，俯视图是等腰直角三角形，有关数据如图所示．
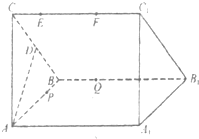（2012•成都一模）设直三梭柱ABC-A1B1C1的底面为等腰直角三角形，AB=AC=2，动点E、F在侧棱CC1上，动点P、Q分别碰AB1，BB1上，若EF═1，CE=x，BQ=y，BP=z，其中x，y，z＞0，则下列结论中错误的是．（ ）
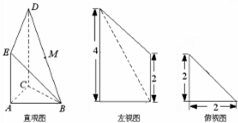（2012•上饶一模）如图是某直三棱柱被削去上底后的直观图与三视图的左视图、俯视图，在直观图中，M是BD的中点，左视图是直角梯形，俯视图是等腰直角三角形，有关数据如图所示．