题目内容
已知a>0,函数f(x)=-2asin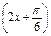 +2a+b,当x∈
+2a+b,当x∈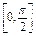 时,-5≤f(x)≤1.
时,-5≤f(x)≤1.
(1)求常数a,b的值;
(2)设g(x)=f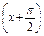 且lg g(x)>0,求g(x)的单调区间.
且lg g(x)>0,求g(x)的单调区间.
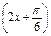 +2a+b,当x∈
+2a+b,当x∈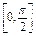 时,-5≤f(x)≤1.
时,-5≤f(x)≤1.(1)求常数a,b的值;
(2)设g(x)=f
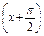 且lg g(x)>0,求g(x)的单调区间.
且lg g(x)>0,求g(x)的单调区间.(1)a=2,b=-5.(2)g(x)的单调减区间为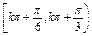 (k∈Z)
(k∈Z)
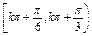 (k∈Z)
(k∈Z)(1)∵x∈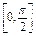 ,∴2x+
,∴2x+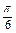 ∈
∈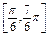 .
.
∴sin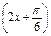 ∈
∈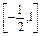 ,
,
∴-2asin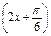 ∈[-2a,a].
∈[-2a,a].
∴f(x)∈[b,3a+b],
又∵-5≤f(x)≤1,因此可得b=-5,3a+b=1,因此a=2,b=-5.
(2)由(1)知a=2,b=-5,
∴f(x)=-4sin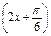 -1,
-1,
g(x)=f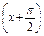 =-4sin
=-4sin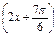 -1
-1
=4sin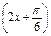 -1.
-1.
又由lg g(x)>0得g(x)>1,∴4sin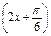 -1>1,
-1>1,
∴sin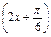 >
>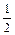 ,
,
∴2k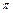 +
+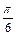 <2x+
<2x+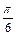 <2k
<2k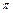 +
+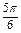 ,k∈Z.
,k∈Z.
由2k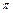 +
+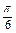 <2x+
<2x+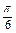 ≤2k
≤2k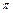 +
+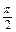 (k∈Z),得g(x)的单调增区间为:
(k∈Z),得g(x)的单调增区间为: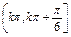 (k∈Z)
(k∈Z)
由2k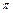 +
+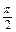 ≤2x+
≤2x+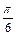 <2k
<2k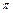 +
+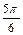 ,
,
得g(x)的单调减区间为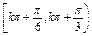 (k∈Z).
(k∈Z).
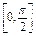 ,∴2x+
,∴2x+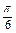 ∈
∈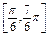 .
.∴sin
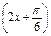 ∈
∈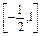 ,
,∴-2asin
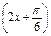 ∈[-2a,a].
∈[-2a,a].∴f(x)∈[b,3a+b],
又∵-5≤f(x)≤1,因此可得b=-5,3a+b=1,因此a=2,b=-5.
(2)由(1)知a=2,b=-5,
∴f(x)=-4sin
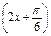 -1,
-1,g(x)=f
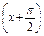 =-4sin
=-4sin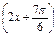 -1
-1=4sin
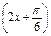 -1.
-1.又由lg g(x)>0得g(x)>1,∴4sin
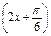 -1>1,
-1>1,∴sin
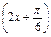 >
>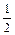 ,
,∴2k
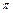 +
+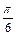 <2x+
<2x+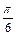 <2k
<2k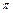 +
+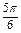 ,k∈Z.
,k∈Z.由2k
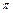 +
+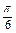 <2x+
<2x+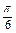 ≤2k
≤2k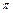 +
+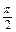 (k∈Z),得g(x)的单调增区间为:
(k∈Z),得g(x)的单调增区间为: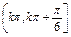 (k∈Z)
(k∈Z)由2k
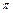 +
+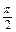 ≤2x+
≤2x+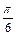 <2k
<2k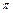 +
+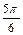 ,
,得g(x)的单调减区间为
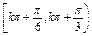 (k∈Z).
(k∈Z).
练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
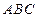 中,内角
中,内角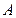 、
、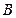 、
、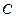 所对的边分别是
所对的边分别是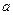 、
、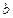 、
、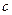 ,已知
,已知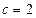 ,
,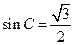 ,
,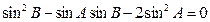 ,求
,求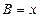 ,△
,△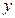 ,试求函数
,试求函数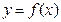 的最大值.
的最大值.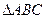 的三边a、b、c所对的角,向量
的三边a、b、c所对的角,向量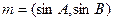 ,
,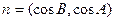 ,且
,且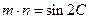 。
。 (1)求角C的大小;
(1)求角C的大小;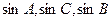 成等差
成等差 数列,且
数列,且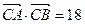 ,求边c的长。
,求边c的长。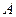 测得一船初始位置
测得一船初始位置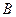 在
在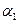 度,
度,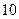 min后船在
min后船在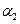 度,船的航向与速度都不变,航向为北偏东
度,船的航向与速度都不变,航向为北偏东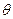 度.求
度.求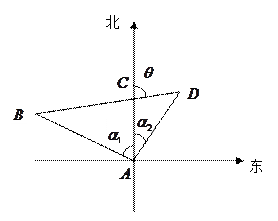
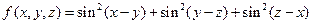 ,
, ,求
,求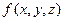 的最大值。
的最大值。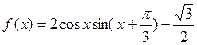 .
.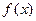 的最小正周期;
的最小正周期;
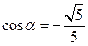 ,
,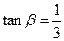 ,
,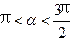 ,
,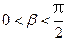 ,求
,求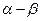 的值.
的值.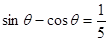 .
. 的值;
的值;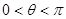 时,求
时,求 的值.
的值.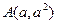 ,
,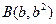
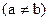 的坐标满足
的坐标满足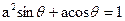 ,
,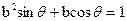 ,则原点到直线AB的距离是___________。
,则原点到直线AB的距离是___________。