题目内容
设{an}是等差数列,若a2=3,a7=13,则数列{an}前8项的和为
- A.128
- B.80
- C.64
- D.56
C
分析:利用等差数列的通项公式,结合已知条件列出关于a1,d的方程组,求出a1,d,代入等差数列的前n项和公式即可求解.或利用等差数列的前n项和公式,结合等差数列的性质a2+a7=a1+a8求解.
解答:解法1:设等差数列{an}的首项为a1,公差为d,
由等差数列的通项公式以及已知条件得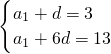 ,
,
解得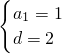 ,故s8=8+
,故s8=8+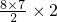 =64.
=64.
解法2:∵a2+a7=a1+a8=16,
∴s8=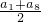 ×8=64.
×8=64.
故选C.
点评:解法1用到了基本量a1与d,还用到了方程思想;
解法2应用了等差数列的性质:{an}为等差数列,当m+n=p+q(m,n,p,q∈N+)时,am+an=ap+aq.
特例:若m+n=2p(m,n,p∈N+),则am+an=2ap.
分析:利用等差数列的通项公式,结合已知条件列出关于a1,d的方程组,求出a1,d,代入等差数列的前n项和公式即可求解.或利用等差数列的前n项和公式,结合等差数列的性质a2+a7=a1+a8求解.
解答:解法1:设等差数列{an}的首项为a1,公差为d,
由等差数列的通项公式以及已知条件得
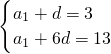 ,
,解得
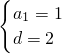 ,故s8=8+
,故s8=8+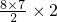 =64.
=64.解法2:∵a2+a7=a1+a8=16,
∴s8=
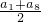 ×8=64.
×8=64.故选C.
点评:解法1用到了基本量a1与d,还用到了方程思想;
解法2应用了等差数列的性质:{an}为等差数列,当m+n=p+q(m,n,p,q∈N+)时,am+an=ap+aq.
特例:若m+n=2p(m,n,p∈N+),则am+an=2ap.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
设{an}是等差数列,a1+a3+a5=9,a6=9.则这个数列的前6项和等于( )
| A、12 | B、24 | C、36 | D、48 |