题目内容
判断以下解法是否正确?如不正确,请指出错误所在,并给出正确解法;如正确,请说出理由.
问题 判断函数y= (a∈R且a≠0)的单调性.
(a∈R且a≠0)的单调性.
解 令x=cosθ,θ∈(0,π),则y=![]()
∵ y=cotθ在(0,π)上是减函数,∴当a>0时,函数为减函数;当a<0时,函数为增函数.
( )
答案:F
解析:
解析:
|
不正解 以上解法是错误的,错误在于将θ误认为是原函数的自变量,其实,函数y=f(x)= ∵x=g(θ)=cosθ(0<θ<π)是减函数,∴当a>0时, |

练习册系列答案
相关题目
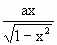 的自变量是x,θ是中间变量,因而必须用判断复合函数的单调性的方法来判断函数y=f(x)=f[g(θ)]的单调性,正确的解法是:
的自变量是x,θ是中间变量,因而必须用判断复合函数的单调性的方法来判断函数y=f(x)=f[g(θ)]的单调性,正确的解法是: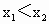 Þ
Þ
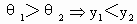 ,∴y=f(x)为增函数;当a<0时,
,∴y=f(x)为增函数;当a<0时,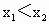 Þ
Þ
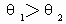 Þ
Þ
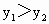 ,∴y=f(x)为减函数.
,∴y=f(x)为减函数.