题目内容
已知k∈R,当k的取值变化时,关于x,y的方程4kx-4y=4-k2的直线有无数条,这无数条直线形成了一个直线系,记集合M={(x,y)|4kx-4y=4-k2仅有唯一直线}.
(1)求M中点(x,y)的轨迹方程;
(2)设P={(x,y)|y=2x+a,a为常数},任取C∈M,D∈P,如果|CD|的最小值为
,求a的值.
(1)求M中点(x,y)的轨迹方程;
(2)设P={(x,y)|y=2x+a,a为常数},任取C∈M,D∈P,如果|CD|的最小值为
| 5 |
分析:(1)由题意易知,k2+4kx-4(y+1)=0仅有唯一解,利用△=16x2+16(y+1)=0,可求M中点(x,y)的轨迹方程;
(2)设直线y=2x+C与轨迹M相切,两方程联立,求出直线方程,利用|CD|的最小值为
,根据点到直线的距离公式,即可求a的值.
(2)设直线y=2x+C与轨迹M相切,两方程联立,求出直线方程,利用|CD|的最小值为
| 5 |
解答:解(1)由题意易知,k2+4kx-4(y+1)=0仅有唯一解,
∴△=16x2+16(y+1)=0,
∴所求的轨迹方程为x2+y+1=0.…..…(3分)
(2)设直线y=2x+C与轨迹M相切,则
由
,消y可得x2+2x+C+1=0,
∴△=4-4(C+1)=0,即C=0,∴y=2x,
∵|CD|的最小值为
,
∴
=
⇒a=±5.…(10分)
∴△=16x2+16(y+1)=0,
∴所求的轨迹方程为x2+y+1=0.…..…(3分)
(2)设直线y=2x+C与轨迹M相切,则
由
|
∴△=4-4(C+1)=0,即C=0,∴y=2x,
∵|CD|的最小值为
| 5 |
∴
| |a| | ||
|
| 5 |
点评:本题考查轨迹方程,考查直线与曲线的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
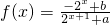 是奇函数.
是奇函数. x3,x∈(-2,2)为正常数.
x3,x∈(-2,2)为正常数.
 (当且仅当a=b时取等号)”推广到三个正数时结论是正确的,试写出推广后的结论(无需证明);
(当且仅当a=b时取等号)”推广到三个正数时结论是正确的,试写出推广后的结论(无需证明);