题目内容
已知：函数f（x）=2ax2+2x-1-a在区间[-1，1]上有且只有一个零点，求：实数a的取值．
解：1°当a=0时，x=
满足题意
2°f（x）=2ax2+2x-1-a是二次函数，则a≠0，对称轴为x=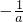
①△=0时不成立
②△＞0时
当a＞0时开口向上∴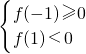
，无解；
当a＜0时开口向下∴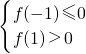
，解得-1＜a＜0
∴实数a的取值是-1＜a≤0．
分析：先确定对称轴属于区间[-1，1]，函数f（x）有唯一解时△=0时不成立；当△大于零0时，分开口向上和向下两种情况讨论．
点评：本题主要考查函数零点问题．注意零点不是点，是函数f（x）=0时x的值．
满足题意2°f（x）=2ax2+2x-1-a是二次函数，则a≠0，对称轴为x=
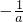
①△=0时不成立
②△＞0时
当a＞0时开口向上∴
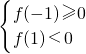，无解；当a＜0时开口向下∴
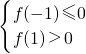，解得-1＜a＜0∴实数a的取值是-1＜a≤0．
分析：先确定对称轴属于区间[-1，1]，函数f（x）有唯一解时△=0时不成立；当△大于零0时，分开口向上和向下两种情况讨论．
点评：本题主要考查函数零点问题．注意零点不是点，是函数f（x）=0时x的值．
练习册系列答案
相关题目