题目内容
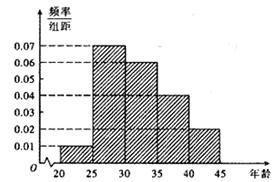
某中学举行了一次“环保知识竞赛”活动.为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照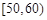 ,
,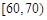 ,
,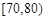 ,
,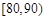 ,
,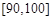 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在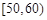 ,
,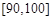 的数据).
的数据).
频率分布直方图 茎叶图
(Ⅰ)求样本容量n和频率分布直方图中x、y的值;
(Ⅱ)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取3名同学到市政广场参加环保知识宣传的志愿者活动,设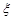 表示所抽取的3名同学中得分在
表示所抽取的3名同学中得分在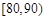 的学生个数,求
的学生个数,求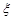 的分布列及其数学期望.
的分布列及其数学期望.
(Ⅰ)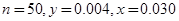 .(Ⅱ)
.(Ⅱ)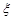 的分布列为:
的分布列为: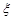
1 2 3 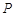
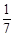
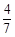
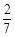
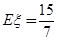 .
.
解析试题分析:(Ⅰ)由频率分布直方图可求出分数在50到60的频率,由茎叶图可得出分数在50到60的人数,
由此可得样本容量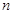 .又由茎叶图可得分数在90到100的人数,从而求得
.又由茎叶图可得分数在90到100的人数,从而求得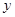 .这样除了60到70分这一组之外,其余各组的频率都知道了,也就可以求出
.这样除了60到70分这一组之外,其余各组的频率都知道了,也就可以求出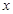 的值了.(Ⅱ)由(Ⅰ)可知,分数在[80,90)有5人,分数在[90,100)有2人,共7人.因为要抽取3人,故至少有一人在
的值了.(Ⅱ)由(Ⅰ)可知,分数在[80,90)有5人,分数在[90,100)有2人,共7人.因为要抽取3人,故至少有一人在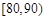 ,所以得分在
,所以得分在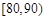 的学生个数
的学生个数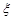 的可能取值为
的可能取值为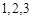 (注意一般情况下是可以取0的),这是一个超几何分布,由此可得
(注意一般情况下是可以取0的),这是一个超几何分布,由此可得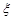 的分布列和期望.
的分布列和期望.
试题解析:(Ⅰ)由题意可知,样本容量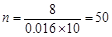 ,
,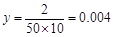 ,
,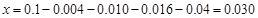 . 3分
. 3分
(Ⅱ)由题意可知,分数在[80,90)有5人,分数在[90,100)有2人,共7人.抽取的3名同学中得分在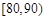 的学生个数
的学生个数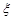 的可能取值为
的可能取值为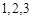 ,则
,则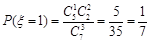 ,
,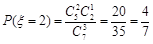 ,
,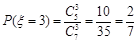 .
.
所以,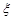 的分布列为
的分布列为
所以,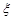
1 2 3 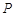
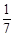
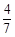
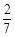
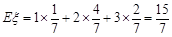 . 12分
. 12分
考点:1、频率分布直方图与茎叶图;2、随机变量的分布列及期望;3、超几何分布.

 阅读快车系列答案
阅读快车系列答案为了解某市民众对政府出台楼市限购令的情况,在该市随机抽取了50名市民进行调查,他们月收入(单位:百元)的频数分布及对楼市限购令赞成的人数如下表:
| 月收入 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(1)根据已知条件完成下面的2×2列联表,问能否在犯错误的概率不超过0.01的前提下认为非高收入族赞成楼市限购令?
| | 非高收入族 | 高收入族 | 合计 |
| 赞成 | | | |
| 不赞成 | | | |
| 合计 | | | |
附:K2=
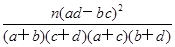
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 |
为了解某班关注NBA是否与性别有关,对本班48人进行了问卷调查得到如下的列联表:
| | 关注NBA | 不关注NBA | 合计 |
| 男生 | | 6 | |
| 女生 | 10 | | |
| 合计 | | | 48 |
 .
.(1)请将上面的表补充完整(不用写计算过程),并判断是否有95%的把握认为关注NBA与性别有关?说明你的理由.
(2)现记不关注NBA的6名男生中某两人为a,b,关注NBA的10名女生中某3人为c,d,e,从这5人中选取2人进行调查,求:至少有一人不关注NBA的被选取的概率。
下面的临界值表,供参考
| P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.005 |
| K | 2.706 | 3.841 | 60635 | 7.879 |
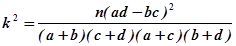 )其中n=a+b+c+d
)其中n=a+b+c+d 根据空气质量指数 (为整数)的不同,可将空气质量分级如下表:
(为整数)的不同,可将空气质量分级如下表:
 (数值) (数值) | 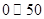 | 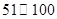 |  |  |  |  |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 空气质量类别颜色 | 绿色 | 黄色 | 橙色 | 红色 | 紫色 | 褐红色 |
 年
年 月
月 日—
日— 月
月 日,对空气质量指数
日,对空气质量指数 进行监测,获得数据后得到如图的条形图
进行监测,获得数据后得到如图的条形图
(1)估计该城市本月(按
 天计)空气质量类别为中度污染的概率;
天计)空气质量类别为中度污染的概率;(2)在上述
 个监测数据中任取
个监测数据中任取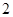 个,设
个,设 为空气质量类别颜色为紫色的天数,求
为空气质量类别颜色为紫色的天数,求 的分布列.
的分布列. 为预防H7N9病毒爆发,某生物技术公司研制出一种H7N9病毒疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个样本分成三组,测试结果如下表:
| 分组 | A组 | B组 | C组 |
| 疫苗有效 | 673 | 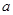 | 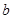 |
| 疫苗无效 | 77 | 90 | 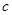 |
(1)现用分层抽样的方法在全体样本中抽取360个测试结果,应在C组抽取样本多少个?
(2)已知
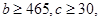 求通过测试的概率.
求通过测试的概率. 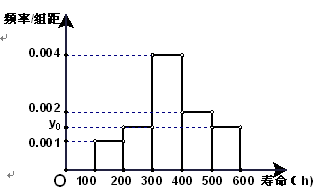
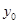 处刻度不清,根据图表所提供的数据还原
处刻度不清,根据图表所提供的数据还原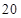 个元件,寿命为
个元件,寿命为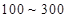 之间的应抽取几个;
之间的应抽取几个; 个元件,求事件“恰好有一个寿命为
个元件,求事件“恰好有一个寿命为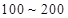 ,一个寿命为
,一个寿命为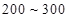 ”的概率.
”的概率.
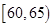 ,
, ,
, ,
, ,
, ,
, 后得到如图的频率分布直方图。问:
后得到如图的频率分布直方图。问:
 中的车辆中任取2辆,求抽出的2辆中速度在
中的车辆中任取2辆,求抽出的2辆中速度在 的分布列及其数学期望。(12分)
的分布列及其数学期望。(12分) ,第2组
,第2组 ,第3组
,第3组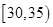 ,第4组
,第4组 ,第5组
,第5组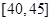 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.