题目内容
如图,用A,B,C,D四类不同的元件接成系统N.当元件A正常工作且元件C,D都正常工作,或者元件A正常工作且元件B正常工作,或者元件A,B,C,D都正常工作时,系统N正常工作.已知元件A,B,C,D正常工作的概率依次为
,
,
,
,则系统N正常工作的概率为

| 2 |
| 3 |
| 3 |
| 4 |
| 3 |
| 4 |
| 4 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |

分析:由题意用A,B,C,D四个不同的元件连接成一个系统N.当元件A正常工作且元件B、C-D至少有一个正常工作时,系统N正常工作.先算出B,C,D至少有一个通的概率,再利用乘法原理求值
解答:解:C,D都工作的概率为
×
=
,记该路能工作为事件E
∵B,E都不工作的概率(1-
)×(1-
)=
故B、E至少有一个正常工作的概率是
又元件A正常工作的概率依次为
故系统N能正常工作的概率等于
×
=
故答案为
| 3 |
| 4 |
| 4 |
| 5 |
| 3 |
| 5 |
∵B,E都不工作的概率(1-
| 3 |
| 5 |
| 3 |
| 4 |
| 1 |
| 10 |
故B、E至少有一个正常工作的概率是
| 9 |
| 10 |
又元件A正常工作的概率依次为
| 2 |
| 3 |
故系统N能正常工作的概率等于
| 2 |
| 3 |
| 9 |
| 10 |
| 3 |
| 5 |
故答案为
| 3 |
| 5 |
点评:本题考查相互独立事件的概率乘法公式,解题的关键是求出B,C所组成的系统能正确常工作的概率,理解并掌握乘法原理是解答本题的知识保证.本题属于概率的应用题,是近几年高考概率的考试方向.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目

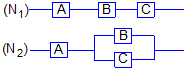 如图,用A、B、C三类不同的元件连接成两个系统N1、N2,当元件A、B、C都正常工作时,系统N1正常工作;当元件A正常工作且元件B、C至少有一个正常工作时,系统N2正常工作.已知元件A、B、C正常工作的概率依次为0.80、0.90、0.90.分别求系统N1、N2正常工作的概率P1、P2.
如图,用A、B、C三类不同的元件连接成两个系统N1、N2,当元件A、B、C都正常工作时,系统N1正常工作;当元件A正常工作且元件B、C至少有一个正常工作时,系统N2正常工作.已知元件A、B、C正常工作的概率依次为0.80、0.90、0.90.分别求系统N1、N2正常工作的概率P1、P2. 如图:用A、B、C、D四类不同的元件连接成系统N,当元件A正常工作且元件B、C都正常工作,或当元件A正常工作且元件D正常工作时,系统N正常工作.已知元件A、B、C、D正常工作的概率依次为
如图:用A、B、C、D四类不同的元件连接成系统N,当元件A正常工作且元件B、C都正常工作,或当元件A正常工作且元件D正常工作时,系统N正常工作.已知元件A、B、C、D正常工作的概率依次为