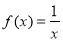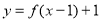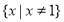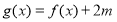题目内容
已知函数
(Ⅰ)判断函数 在
在 上的单调性,并用定义加以证明;
上的单调性,并用定义加以证明;
(Ⅱ)若对任意 ,总存在
,总存在 ,使得
,使得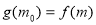 成立,求实数
成立,求实数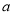 的取值范围
的取值范围
(Ⅰ)函数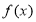 在
在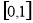 上的单调递增 (Ⅱ)实数
上的单调递增 (Ⅱ)实数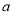 的取值范围
的取值范围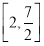
【解析】
试题分析:(Ⅰ)利用函数的单调性的定义判断:先由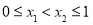 ,然后利用
,然后利用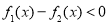 判断出单调性,本题的关键在于:先把
判断出单调性,本题的关键在于:先把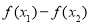 转化成因式乘积的形式
转化成因式乘积的形式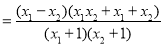 ,继而判断每一个因式的符号,最后得到
,继而判断每一个因式的符号,最后得到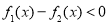 ,即
,即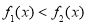
(Ⅱ)先由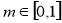 ,得到
,得到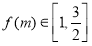 ,然后利用
,然后利用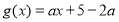 在
在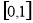 上的单调递增,得到
上的单调递增,得到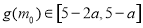 ,只需
,只需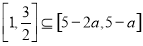 ,利用子集的性质得到
,利用子集的性质得到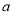 的取值范围
的取值范围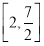
试题解析:(Ⅰ)函数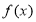 在
在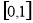 上的单调递增 1分
上的单调递增 1分
证明如下:设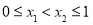 ,则
,则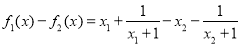
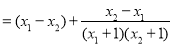
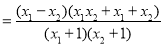 2分
2分
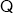
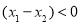 ,
,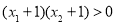 ,
,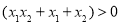

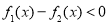 ,即
,即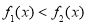 , 2分
, 2分
 函数
函数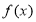 在
在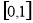 上的单调递增 1分
上的单调递增 1分
(Ⅱ)由(Ⅰ)知,当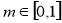 时,
时,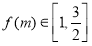 , 1分
, 1分
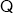
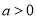 ,
,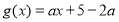 在
在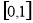 上的单调递增,
上的单调递增,

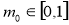 时,
时,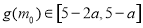 1分
1分
依题意,只需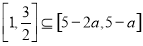 2分
2分

 ,解得
,解得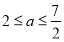 ,即 实数
,即 实数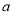 的取值范围
的取值范围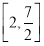 2分
2分
考点:1、函数的单调性的定义;2、一次函数求值域;3、利用子集的性质

练习册系列答案
相关题目