Question

设f（x）为定义在R上的偶函数，当x＜-1时，f（x）=x+m，且f（x）的图象经过点（-2，0）；当-1≤x≤0时，f（x）的图象是顶点在（0，2），过点（-1，1）且开口向下的抛物线的一部分．则函数的表达式为

f(x)=

-x+2(x＞1) -x2+2(-1≤x≤1) x+2(x＜-1)

．

Answer 1

分析：由题意知，x≤-1时，用点斜式求得，x≥1时用偶函数求得，-1＜x＜1时，用待定系数法求得函数的解析式即可．

解答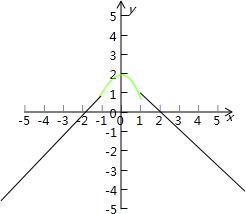：解：经过点（-2，0），斜率为1的射线：y=x+2   （x≤-1）
抛物线过（-1，1）和（0，2）
令y=ax²+c
代入，得y=-x²+2   （-1＜x＜1）
又函数在R上是偶函数
所以x≥1时，射线经过（2，0）且斜率为-1
即y=-x+2  （x≥1）
所以 f(x)=

-x+2(x＞1) -x2+2(-1≤x≤1) x+2(x＜-1)

，
故答案为：f(x)=

-x+2(x＞1) -x2+2(-1≤x≤1) x+2(x＜-1)

．

点评：本题主要考查分段函数及函数的图象、函数奇偶性的应用、待定系数当等基础知识，考查运算求解能力，考查数形结合思想，属于基础题．