题目内容
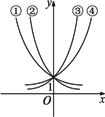
如图，图中所示是指数函数①y＝ax，②y＝bx，③y＝cx，④y＝dx的图象，则a、b、c、d与1的大小关系是
[ ]
A．a＜b＜1＜c＜d
B．b＜a＜1＜d＜c
C．1＜a＜b＜c＜d
D．a＜b＜1＜d＜c
答案：B
解析：
提示：
解析：
|
解：因为当指数函数底数大于1时，图象呈上升趋势，且底数越大，图象向上方向越靠近y轴；当指数函数底数大于0且小于1时，图象呈下降趋势，且底数越小，图象向右方向越靠近x轴；所以，根据题目所给图象，应该选择B． 点评：运用上述方法有利于弄清指数函数在第一象限的图象的大致变化情形．本题除了可以运用上述方法来解以外，还可以运用下面的方法来解： (1)令x＝1，则题目所给四个函数的函数值分别为a、b、c、d，结合函数图象，就可得到解答．应该选择B． (2)在所给图象中，过点(1，0)作x轴的垂线，则垂线与图象的交点的纵坐标就是函数当x＝1时的函数值，分别为a、b、c、d，因此，根据函数的图象不难得到本题的答案． |
提示：
|
根据指数函数的图象和性质，可将题目所给四个函数的底数进行分类一类是底数大于1，另一类是底数大于0小于1，然后在同一类中比较大小． |
练习册系列答案
教学练新同步练习系列答案
相关题目
某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中，发现其注意力指数P与听课时间t之间的关系满足如图所示的曲线．当t∈（0，14]时，曲线是二次函数图象的一部分，当t∈[14，40]时，曲线是函数y=logα（x-5）+83（a＞0且a≠1）图象的一部分．根据专家研究，当注意力指数P大于等于80时听课效果最佳．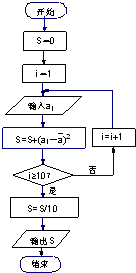
某市新年第一个月前10天监测到空气污染指数如下表（主要污染物为可吸入颗粒物）：（第i天监测得到的数据记为ai）
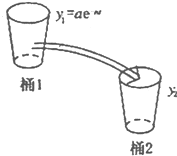（2009•河北区二模）如图所示，桶1中的水按一定规律流入桶2中，已知开始时桶1中有a升水，桶2是空的，t分钟后桶1中剩余的水符合指数衰减曲线
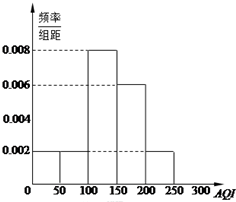根据我国发布的《环境空气质量指数AQI技术规定》（试行），AQI共分为六级：[0，50）为优，[50，100）为良，[100，150）为轻度污染，[150，200）为中度污染，[200，250），[250，300）均为重度污染，300及以上为严重污染．某市2013年11月份30天的AQI的频率分布直方图如图所示：
与听课时间
之间的关系满足如图所示的曲线．当
时，曲线是二次函数图象的一部分，
为其对称轴；当
时，曲线是函数
(
且
)图象的一部分．根据专家研究，当注意力指数
的函数关系式；