题目内容
已知函数g(x)=Asin(wx+φ)(A>0,w>0,0<φ<π)的图象如图所示,其中点A(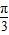 ,2)、B(
,2)、B(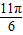 ,0)分别是函数的最大值点和零点.
,0)分别是函数的最大值点和零点.(I)求函数y=g(x)的解析式;
(Ⅱ)若函数f(x)=2g(x)cosx+m在[0,
 ]上的最大值为6,求函数f(x)在R上的最小值及相应的x值的集合.
]上的最大值为6,求函数f(x)在R上的最小值及相应的x值的集合.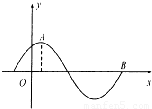
【答案】分析:(Ⅰ)根据图象可知 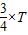 =
=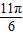 -
-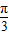 ,解得T的值,进而求得w,再根据顶点坐标可得A=2,将点A点的坐标代入函数y=g(x),可得sin(
,解得T的值,进而求得w,再根据顶点坐标可得A=2,将点A点的坐标代入函数y=g(x),可得sin(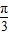 +φ)=1,结合0<φ<π求得 φ,从而得到函数解析式.
+φ)=1,结合0<φ<π求得 φ,从而得到函数解析式.
(Ⅱ)根据两角和差的正弦函数化简f(x)的解析式为2sin(2x+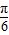 )+m+1,根据x的范围求得f(x)的最大值为2+m+1=6,求得m的值,即可确定f(x)的解析式,由此求得函数取得最小值时x值的集合.
)+m+1,根据x的范围求得f(x)的最大值为2+m+1=6,求得m的值,即可确定f(x)的解析式,由此求得函数取得最小值时x值的集合.
解答:解:(Ⅰ)根据图象可知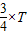 =
=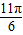 -
- ,解得T=2π. 再由
,解得T=2π. 再由  =2π,可得w=1.
=2π,可得w=1.
由顶点坐标可得A=2,所以,g(x)=2sin(x+φ),
将点A点的坐标代入函数y=g(x),可得sin(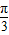 +φ)=1,∴
+φ)=1,∴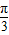 +φ=2kπ+
+φ=2kπ+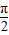 ,k∈z.
,k∈z.
再结合0<φ<π求得 φ=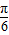 .
.
所以,g(x)=2sin(x+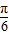 ).…(6分)
).…(6分)
(Ⅱ)f(x)=2g(x)cosx+m=4sin(x+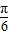 )cosx+m=4(
)cosx+m=4(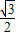 sinx+
sinx+ cosx)cosx+m
cosx)cosx+m
=2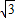 sinxcosx+2cos2x+m=
sinxcosx+2cos2x+m=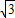 sin2x+2cos2x+1+m=2sin(2x+
sin2x+2cos2x+1+m=2sin(2x+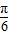 )+m+1.…(9分)
)+m+1.…(9分)
由x∈[0,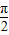 ],得 2x+
],得 2x+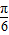 ∈[
∈[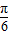 ,
,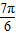 ],于是函数f(x)的最大值为2+m+1=6,解得m=3.
],于是函数f(x)的最大值为2+m+1=6,解得m=3.
所以f(x)=2sin(2x+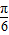 )+4.
)+4.
当x∈R时,f(x)的最小值为-2+4=2,此时x满足2x+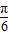 =2kπ+
=2kπ+ ,k∈z,
,k∈z,
相应的x值的集合为{x|x=kπ+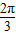 ,k∈z}.…(12分)
,k∈z}.…(12分)
点评:本题主要考查由函数y=Asin(ωx+∅)的部分图象求解析式,两角和差的正弦函数,正弦函数的定义域和值域,属于中档题.
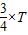 =
=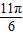 -
-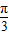 ,解得T的值,进而求得w,再根据顶点坐标可得A=2,将点A点的坐标代入函数y=g(x),可得sin(
,解得T的值,进而求得w,再根据顶点坐标可得A=2,将点A点的坐标代入函数y=g(x),可得sin(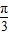 +φ)=1,结合0<φ<π求得 φ,从而得到函数解析式.
+φ)=1,结合0<φ<π求得 φ,从而得到函数解析式.(Ⅱ)根据两角和差的正弦函数化简f(x)的解析式为2sin(2x+
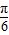 )+m+1,根据x的范围求得f(x)的最大值为2+m+1=6,求得m的值,即可确定f(x)的解析式,由此求得函数取得最小值时x值的集合.
)+m+1,根据x的范围求得f(x)的最大值为2+m+1=6,求得m的值,即可确定f(x)的解析式,由此求得函数取得最小值时x值的集合.解答:解:(Ⅰ)根据图象可知
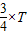 =
=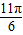 -
- ,解得T=2π. 再由
,解得T=2π. 再由  =2π,可得w=1.
=2π,可得w=1.由顶点坐标可得A=2,所以,g(x)=2sin(x+φ),
将点A点的坐标代入函数y=g(x),可得sin(
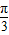 +φ)=1,∴
+φ)=1,∴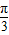 +φ=2kπ+
+φ=2kπ+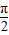 ,k∈z.
,k∈z.再结合0<φ<π求得 φ=
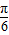 .
.所以,g(x)=2sin(x+
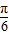 ).…(6分)
).…(6分)(Ⅱ)f(x)=2g(x)cosx+m=4sin(x+
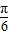 )cosx+m=4(
)cosx+m=4(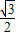 sinx+
sinx+ cosx)cosx+m
cosx)cosx+m=2
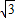 sinxcosx+2cos2x+m=
sinxcosx+2cos2x+m=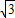 sin2x+2cos2x+1+m=2sin(2x+
sin2x+2cos2x+1+m=2sin(2x+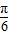 )+m+1.…(9分)
)+m+1.…(9分)由x∈[0,
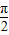 ],得 2x+
],得 2x+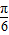 ∈[
∈[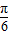 ,
,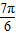 ],于是函数f(x)的最大值为2+m+1=6,解得m=3.
],于是函数f(x)的最大值为2+m+1=6,解得m=3.所以f(x)=2sin(2x+
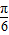 )+4.
)+4.当x∈R时,f(x)的最小值为-2+4=2,此时x满足2x+
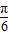 =2kπ+
=2kπ+ ,k∈z,
,k∈z,相应的x值的集合为{x|x=kπ+
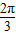 ,k∈z}.…(12分)
,k∈z}.…(12分)点评:本题主要考查由函数y=Asin(ωx+∅)的部分图象求解析式,两角和差的正弦函数,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目