题目内容

已知函数f（x）=x|x-a|-2，若当x∈（0，1]时，恒有f（x）≤0，则a的最大值是（　　）
分析：先将原函数式化为分段函数的形式：f（x）=x|x-a|-2=
x(x-a)-2，x＞a
-x(x-a)-2，x≤a
，画出它的示意图，如图，由于只须求a的最大值，下面只须考察a＞2时，当x∈（0，1]时，恒有f（x）≤0成立的条件，利用函数在（0，1]上是增函数，即可得出a的最大值
解答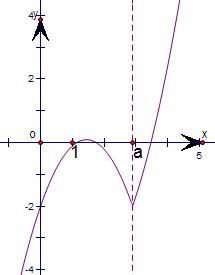：解：原函数式化为：f（x）=x|x-a|-2=
x(x-a)-2，x＞a
-x(x-a)-2，x≤a
，
画出它的示意图，如图，
下面只须考察a＞2时，当x∈（0，1]时，恒有f（x）≤0成立的条件，
由图可知，当a＞2时，函数在（0，1]上是增函数，
故只须f（1）≤0，即-1×（1-a）-2≤0，
a≤3，
则a的最大值是3，
故选A．
点评：本小题主要考查函数单调性的应用、带绝对值的函数、不等式的解法等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．
练习册系列答案
相关题目
精英家教网已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜
π
2
）的部分图象如图所示，则f（x）的解析式是（　　）
A、f(x)=2sin(πx+
π
6
)(x∈R)
B、f(x)=2sin(2πx+
π
6
)(x∈R)
C、f(x)=2sin(πx+
π
3
)(x∈R)
D、f(x)=2sin(2πx+
π
3
)(x∈R)
（2012•深圳一模）已知函数f(x)=
1
3
x3+bx2+cx+d，设曲线y=f（x）在与x轴交点处的切线为y=4x-12，f′（x）为f（x）的导函数，且满足f′（2-x）=f′（x）．
（1）求f（x）；
（2）设g(x)=x
f′(x)
 ， m＞0，求函数g（x）在[0，m]上的最大值；
（3）设h（x）=lnf′（x），若对一切x∈[0，1]，不等式h（x+1-t）＜h（2x+2）恒成立，求实数t的取值范围．
（2011•上海模拟）已知函数f(x)=(
x
a
-1)2+(
b
x
-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k2，b=（k+c）2时，记f（x）=f1（x）；当a=（k+c）2，b=（k+2c）2时，记f（x）=f2（x）．
求证：f1(x)+f2(x)＞
4c2
k(k+c)
．
已知函数f(x)=(
x
a
-1)2+(
b
x
-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k2，b=（k+c）2时，记f（x）=f1（x）；当a=（k+c）2，b=（k+2c）2时，记f（x）=f2（x）．
求证：f1(x)+f2(x)＞
4c2
k(k+c)
．
已知函数f(x)=
1
3
x3+bx2+cx+d，设曲线y=f（x）在与x轴交点处的切线为y=4x-12，f′（x）为f（x）的导函数，且满足f′（2-x）=f′（x）．
（1）求f（x）；
（2）设g(x)=x
f′(x)
 ， m＞0，求函数g（x）在[0，m]上的最大值；
（3）设h（x）=lnf′（x），若对一切x∈[0，1]，不等式h（x+1-t）＜h（2x+2）恒成立，求实数t的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网