题目内容
(本小题满分12分)
已知函数 (
( 为实数,
为实数, ,
, ),若
),若 ,且函数
,且函数 的值域为
的值域为 .
.
(1)求 的表达式;
的表达式;
(2)当 时,
时, 是单调函数,求实数
是单调函数,求实数 的取值范围.
的取值范围.
【答案】
解:
(1) ;(2)
;(2)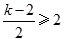 或
或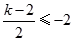 时
时 单调。
单调。
【解析】
试题分析:(1)根据题意分析得到函数a,b的关系式,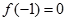 ,所以
,所以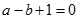 .,同时利用
.,同时利用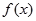 的值域为
的值域为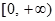 ,说明判别式为零。
,说明判别式为零。
(2)根据对称轴和定义域的关系,来得到参数的范围。
解:
(1)因为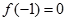 ,所以
,所以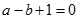 .
.
因为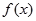 的值域为
的值域为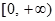 ,所以
,所以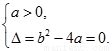 .................3分
.................3分
所以 .
解得
.
解得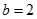 ,
,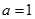 .
所以
.
所以 ....................6分
....................6分
(2)因为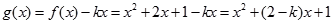
=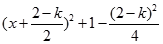 ,..................................8分
,..................................8分
所以当 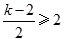 或
或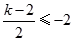 时
时 单调.................................12分
单调.................................12分
考点:本试题主要考查了二次函数解析式的求解,以及单调性的运用。
点评:解决该试题的关键是通过函数的值域,得到最小值为0,进而确定出判别式为零。那么再结合对称轴和定义域的关系得到参数的范围。

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目