题目内容
已知正四棱锥P-ABCD的主视图和左视图均为边长是2的正三角形，俯视图是边长为2的正方形，则此正四棱锥的体积是
．
4
| ||
| 3 |
4
| ||
| 3 |
分析：三视图复原的几何体是正四棱锥，求出底面面积，正四棱锥的高，即可求出体积．
解答：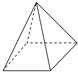
解：如图据条件可得几何体为底面边长为2的正方形，侧面是等边三角形的高为2的正四棱锥，
正四棱锥的高为：
，
故其体积故其体积V=
×4×
=
．
故答案为：
解：如图据条件可得几何体为底面边长为2的正方形，侧面是等边三角形的高为2的正四棱锥，正四棱锥的高为：
| 22-1 |
故其体积故其体积V=
| 1 |
| 3 |
| 22-1 |
4
| ||
| 3 |
故答案为：
4
| ||
| 3 |
点评：本题是基础题，考查几何体的三视图，几何体的体积的求法，准确判断几何体的形状是解题的关键．
练习册系列答案
初中学业考试导与练系列答案
相关题目
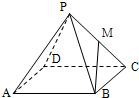
已知正四棱锥P-ABCD的全面积为2，记正四棱锥的高为h．
,M是侧棱PC的中点,则异面直线PA与BM所成角的大小为__________.
已知正四棱锥P-ABCD的全面积为2，记正四棱锥的高为h．
，M是侧棱PC的中点，则异面直线PA与BM所成角为 ．