题目内容
(本小题共14分)
已知函数![]() 与
与![]() 的图象相交于
的图象相交于![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的图象在
的图象在![]() 两点的切线,
两点的切线,![]() 分别是
分别是![]() ,
,![]() 与
与![]() 轴的交点.
轴的交点.
(I)求![]() 的取值范围;
的取值范围;
(II)设![]() 为点
为点![]() 的横坐标,当
的横坐标,当![]() 时,写出
时,写出![]() 以
以![]() 为自变量的函数式,并求其定义域和值域;
为自变量的函数式,并求其定义域和值域;
(III)试比较![]() 与
与![]() 的大小,并说明理由(
的大小,并说明理由(![]() 是坐标原点).
是坐标原点).
解析:(I)由方程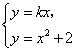 消
消![]() 得
得![]() .???? ①
.???? ①
依题意,该方程有两个正实根,
故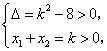 解得
解得![]() .
.
(II)由![]() ,求得切线
,求得切线![]() 的方程为
的方程为![]() ,
,
由![]() ,并令
,并令![]() ,得
,得![]()
![]() ,
,![]() 是方程①的两实根,且
是方程①的两实根,且![]() ,故
,故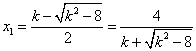 ,
,![]() ,
,
![]() 是关于
是关于![]() 的减函数,所以
的减函数,所以![]() 的取值范围是
的取值范围是![]() .
.
![]() 是关于
是关于![]() 的增函数,定义域为
的增函数,定义域为![]() ,所以值域为
,所以值域为![]() ,
,
(III)当![]() 时,由(II)可知
时,由(II)可知![]() .
.
类似可得![]() .
.![]() .
.
由①可知![]() .
.
从而![]() .
.
当![]() 时,有相同的结果
时,有相同的结果![]() .
.
所以![]() .
.

练习册系列答案
相关题目
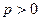 ,动点
,动点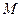 到定点
到定点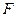
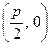 的距离比
的距离比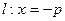 的距离小
的距离小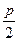 .
.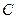 的方程;
的方程; 是轨迹
是轨迹 的两个不同点,
的两个不同点,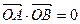 ,求
,求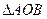 面积的最小值;
面积的最小值;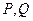 关于直线
关于直线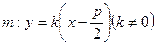 对称?若存在,求出直线
对称?若存在,求出直线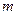 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.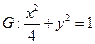 .过点(m,0)作圆
.过点(m,0)作圆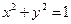 的切线l交椭圆G于A,B两点.
的切线l交椭圆G于A,B两点.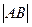 表示为m的函数,并求
表示为m的函数,并求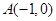 ,
,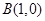 ,动点P满足
,动点P满足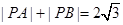 ,记动点P的轨迹为W.
,记动点P的轨迹为W.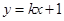 与曲线W交于不同的两点C,D,若存在点
与曲线W交于不同的两点C,D,若存在点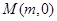 ,使得
,使得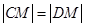 成立,求实数m的取值范围.
成立,求实数m的取值范围.