题目内容
在xoy平面上,四边形ABCD的四个顶点坐标依次为(0,0),(1,0),(2,1)及(0,3),则这个四边形绕x轴旋转一周所得到的几何体的体积为分析:根据已知中四边形ABCD的四个顶点坐标依次为(0,0),(1,0),(2,1)及(0,3),画出满足条件的平面图形,根据旋转体的定义,分析旋转后形成几何体的形状,然后代入体积公式即可求解.
解答: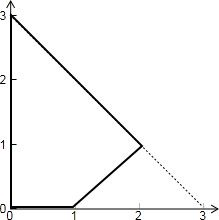 解:满足条件的四个点位置如下图所示:
解:满足条件的四个点位置如下图所示:
这个四边形绕x轴旋转一周所得到的几何体是一个:
以3为底面半径以3为高的大圆锥,
挖掉两个以1为底面半径,以1为高的小圆锥,
故V=
•π•32•3-2•
•π•12•1
=
故答案:
.
 解:满足条件的四个点位置如下图所示:
解:满足条件的四个点位置如下图所示:这个四边形绕x轴旋转一周所得到的几何体是一个:
以3为底面半径以3为高的大圆锥,
挖掉两个以1为底面半径,以1为高的小圆锥,
故V=
| 1 |
| 3 |
| 1 |
| 3 |
=
| 25π |
| 3 |
故答案:
| 25π |
| 3 |
点评:本题考查的知识点是组合体的几何体的体积问题,根据已知条件画出图形,分析出四边形绕x轴旋转一周所得到的几何体的形状是解答本题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目