题目内容
将圆
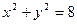 上的点的横坐标保持不变,纵坐标变为原来的
上的点的横坐标保持不变,纵坐标变为原来的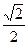 倍,得到曲线
倍,得到曲线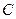 .设直线
.设直线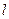 与曲线
与曲线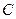 相交于
相交于 、
、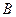 两点,且
两点,且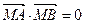 ,其中
,其中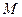 是曲线
是曲线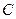 与
与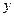 轴正半轴的交点.
轴正半轴的交点.(Ⅰ)求曲线
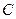 的方程;
的方程;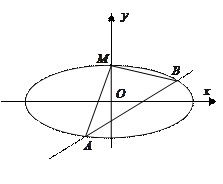 (Ⅱ)证明:直线
(Ⅱ)证明:直线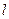 的纵截距为定值.
的纵截距为定值.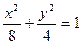 ;
;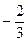
(Ⅰ)设所求曲线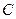 上的任一点坐标为
上的任一点坐标为 ,圆
,圆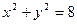 上的对应点的坐标为
上的对应点的坐标为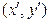 ,由题意可得
,由题意可得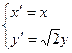 ,
,
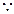
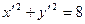 ,
,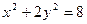 ,即
,即
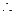 曲线
曲线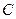 的方程为
的方程为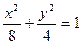 .
.
 (Ⅱ)
(Ⅱ)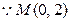 ,显然直线
,显然直线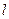 与
与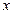 轴不垂直,设直线
轴不垂直,设直线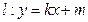 ,与椭圆
,与椭圆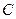 :
: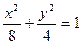 相交于
相交于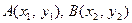 ,
,
由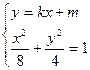 得
得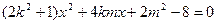 ,
,
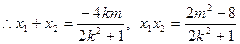 ,
, 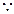
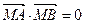 ,
,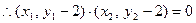 ,
,
即: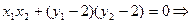
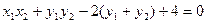 ,
,
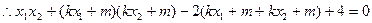 ,
,
整理得: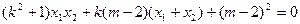 ,
,
即 ,
,
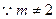 ,
,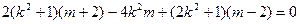 ,
,
展开得: ,
, ,
,
 直线
直线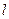 的纵截距为定值
的纵截距为定值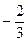 .
.
 上的任一点坐标为
上的任一点坐标为 ,圆
,圆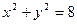 上的对应点的坐标为
上的对应点的坐标为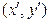 ,由题意可得
,由题意可得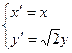 ,
, 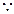
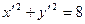 ,
,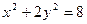 ,即
,即  曲线
曲线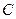 的方程为
的方程为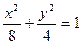 .
.  (Ⅱ)
(Ⅱ)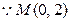 ,显然直线
,显然直线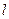 与
与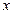 轴不垂直,设直线
轴不垂直,设直线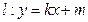 ,与椭圆
,与椭圆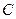 :
: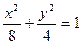 相交于
相交于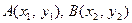 ,
,由
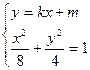 得
得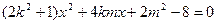 ,
, 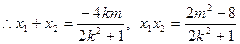 ,
, 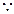
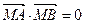 ,
,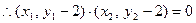 ,
,即:
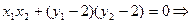
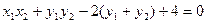 ,
,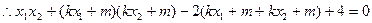 ,
,整理得:
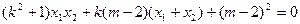 ,
, 即
 ,
,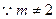 ,
,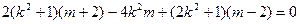 ,
,展开得:
 ,
, ,
, 直线
直线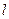 的纵截距为定值
的纵截距为定值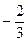 .
. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,相应于焦点F(c,0)(c>0)的准线
,相应于焦点F(c,0)(c>0)的准线 与x轴交于点A,且|OF|=3|OA|,过点F的直线与双曲线交于P、Q两点.
与x轴交于点A,且|OF|=3|OA|,过点F的直线与双曲线交于P、Q两点. =0,求直线PQ的方程.
=0,求直线PQ的方程.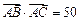 .
.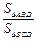 的值.
的值.
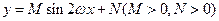 在区间
在区间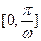 上截直线
上截直线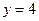 与
与 所得的弦长相等且不为0,则下列描述中正确的是 ( )
所得的弦长相等且不为0,则下列描述中正确的是 ( )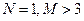
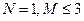


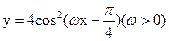 的图象与直线y=3在y轴右侧的交点按横坐标从小到大依次为P1,P2,P3,…,若
的图象与直线y=3在y轴右侧的交点按横坐标从小到大依次为P1,P2,P3,…,若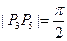 ,则
,则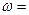 。
。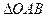
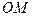

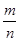 x+
x+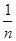 的图象同时经过第一、三、四象限的必要不充分条件是( )
的图象同时经过第一、三、四象限的必要不充分条件是( )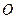 的半径为
的半径为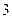 ,从圆
,从圆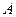 引切线
引切线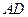 和割线
和割线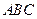 ,
,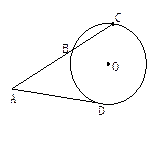

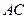 的距离为
的距离为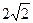 ,
,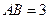 ,则切线
,则切线