题目内容
已知函数 (其中e是自然对数的底数)
(其中e是自然对数的底数)(1)若f(x)是奇函数,求实数a的值;
(2)若函数y=|f(x)|在[0,1]上单调递增,试求实数a的取值范围;
(3)设函数
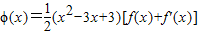 ,求证:对于任意的t>-2,总存在x∈(-2,t),满足
,求证:对于任意的t>-2,总存在x∈(-2,t),满足 ,并确定这样的x的个数.
,并确定这样的x的个数.
【答案】分析:(1)利用f(0)=0即可求出a的值.
(2)通过对a分类讨论和利用单调增函数的定义即可求出a的取值范围.
(3)已知问题:对于任意的t>-2,总存在x∈(-2,t),满足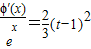 ,等价于证明:对任意的t>-2,方程
,等价于证明:对任意的t>-2,方程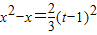 在区间(-2,t)内有实数解,通过对t分类讨论即可.
在区间(-2,t)内有实数解,通过对t分类讨论即可.
解答:解:(1)∵函数f(x)是实数集R上的奇函数,∴f(0)=0,∴1+a=0,解得a=-1.
∴f(x)=ex-e-x,经验证函数f(x)是R上的奇函数.
故a=-1适合题意.
(2)a=0时,y=ex在区间[0,1]上单调递增,适合题意;
当a≠0时,令t=ex,∵x∈[0,1],∴t∈[1,e].且t=ex单调递增,故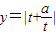 在t∈[1,e]时递增.
在t∈[1,e]时递增.
当a>0时,函数y= 在t∈[1,e]时单调递增,得
在t∈[1,e]时单调递增,得 ,∴0<a≤1.
,∴0<a≤1.
当a<0时, 在t∈[1,e]时单调递增恒成立,故?t∈[1,e],
在t∈[1,e]时单调递增恒成立,故?t∈[1,e], .
.
∴-1≤a<0.
综上可知:-1≤a≤1.
(3)∵f(x)+f′(x)= =2ex,∴φ(x)=(x2-3x+3)ex,∴
=2ex,∴φ(x)=(x2-3x+3)ex,∴ =x2-x.
=x2-x.
要证明:对于任意的t>-2,总存在x∈(-2,t),满足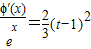 .
.
等价于证明:对任意的t>-2,方程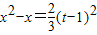 在区间(-2,t)内有实数解.
在区间(-2,t)内有实数解.
令g(x)=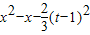 ,
,
则g(-2)=6-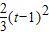 =-
=-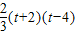 ,g(t)=
,g(t)=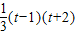 .
.
所以①当t>4,或-2<t<1时,g(-2)g(t)<0,
∴g(x)=0在(-2,t)内有解,且只有一解.
②当1<t<4时,g(-2)>0,且g(t)>0,但g(0)=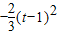 <0,
<0,
∴g(x)=0在(-2,t)内有解,且由两解.
③当t=1时,有且只有一个解x=0;
当t=4时,有且只有一个解x=3.
综上所述:对于任意的t>-2,总存在x∈(-2,t),满足 .
.
且当t≥4或-2<≤1时,有唯一的x适合题意;
当1<t<4时,有两个不同的x适合题意.
点评:充分理解函数的单调性及分类讨论的思想方法是解题的关键.
(2)通过对a分类讨论和利用单调增函数的定义即可求出a的取值范围.
(3)已知问题:对于任意的t>-2,总存在x∈(-2,t),满足
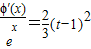 ,等价于证明:对任意的t>-2,方程
,等价于证明:对任意的t>-2,方程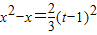 在区间(-2,t)内有实数解,通过对t分类讨论即可.
在区间(-2,t)内有实数解,通过对t分类讨论即可.解答:解:(1)∵函数f(x)是实数集R上的奇函数,∴f(0)=0,∴1+a=0,解得a=-1.
∴f(x)=ex-e-x,经验证函数f(x)是R上的奇函数.
故a=-1适合题意.
(2)a=0时,y=ex在区间[0,1]上单调递增,适合题意;
当a≠0时,令t=ex,∵x∈[0,1],∴t∈[1,e].且t=ex单调递增,故
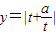 在t∈[1,e]时递增.
在t∈[1,e]时递增.当a>0时,函数y=
 在t∈[1,e]时单调递增,得
在t∈[1,e]时单调递增,得 ,∴0<a≤1.
,∴0<a≤1.当a<0时,
 在t∈[1,e]时单调递增恒成立,故?t∈[1,e],
在t∈[1,e]时单调递增恒成立,故?t∈[1,e], .
.∴-1≤a<0.
综上可知:-1≤a≤1.
(3)∵f(x)+f′(x)=
 =2ex,∴φ(x)=(x2-3x+3)ex,∴
=2ex,∴φ(x)=(x2-3x+3)ex,∴ =x2-x.
=x2-x.要证明:对于任意的t>-2,总存在x∈(-2,t),满足
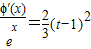 .
.等价于证明:对任意的t>-2,方程
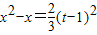 在区间(-2,t)内有实数解.
在区间(-2,t)内有实数解.令g(x)=
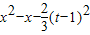 ,
,则g(-2)=6-
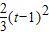 =-
=-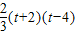 ,g(t)=
,g(t)=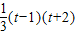 .
.所以①当t>4,或-2<t<1时,g(-2)g(t)<0,
∴g(x)=0在(-2,t)内有解,且只有一解.
②当1<t<4时,g(-2)>0,且g(t)>0,但g(0)=
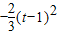 <0,
<0,∴g(x)=0在(-2,t)内有解,且由两解.
③当t=1时,有且只有一个解x=0;
当t=4时,有且只有一个解x=3.
综上所述:对于任意的t>-2,总存在x∈(-2,t),满足
 .
.且当t≥4或-2<≤1时,有唯一的x适合题意;
当1<t<4时,有两个不同的x适合题意.
点评:充分理解函数的单调性及分类讨论的思想方法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
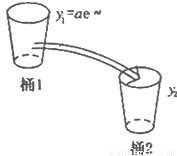
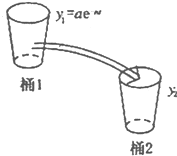 (2009•河北区二模)如图所示,桶1中的水按一定规律流入桶2中,已知开始时桶1中有a升水,桶2是空的,t分钟后桶1中剩余的水符合指数衰减曲线
(2009•河北区二模)如图所示,桶1中的水按一定规律流入桶2中,已知开始时桶1中有a升水,桶2是空的,t分钟后桶1中剩余的水符合指数衰减曲线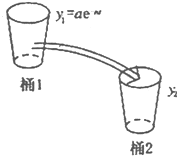 如图所示,桶1中的水按一定规律流入桶2中,已知开始时桶1中有a升水,桶2是空的,t分钟后桶1中剩余的水符合指数衰减曲线
如图所示,桶1中的水按一定规律流入桶2中,已知开始时桶1中有a升水,桶2是空的,t分钟后桶1中剩余的水符合指数衰减曲线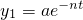 (其中n是常数,e是自对数的底数).假设在经过5分钟时,桶1和桶2中的水恰好相等.求:
(其中n是常数,e是自对数的底数).假设在经过5分钟时,桶1和桶2中的水恰好相等.求: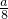 ?
?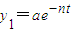 (其中n是常数,e是自对数的底数).假设在经过5分钟时,桶1和桶2中的水恰好相等.求:
(其中n是常数,e是自对数的底数).假设在经过5分钟时,桶1和桶2中的水恰好相等.求: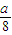 ?
?