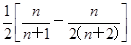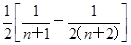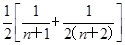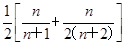题目内容
已知数列{an}是首项为1,公差为20的等差数列,数列{bn}是首项为1,公比为3的等比数列,则数列{an·bn}的前n项和为________.
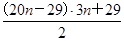
an=1+20(n-1)=20n-19,
bn=3n-1,
令Sn=1×1+21×3+41×32+…+(20n-19)·3n-1,①
则3Sn=1×3+21×32+…+(20n-39)·3n-1+(20n-19)·3n,②
①-②得,-2Sn=1+20×(3+32+…+3n-1)-(20n-19)·3n=1+20×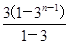 -(20n-19)·3n=(29-20n)·3n-29,
-(20n-19)·3n=(29-20n)·3n-29,
所以Sn=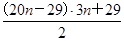
bn=3n-1,
令Sn=1×1+21×3+41×32+…+(20n-19)·3n-1,①
则3Sn=1×3+21×32+…+(20n-39)·3n-1+(20n-19)·3n,②
①-②得,-2Sn=1+20×(3+32+…+3n-1)-(20n-19)·3n=1+20×
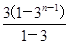 -(20n-19)·3n=(29-20n)·3n-29,
-(20n-19)·3n=(29-20n)·3n-29,所以Sn=
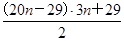

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 (常数
(常数 ),其前
),其前 项和为
项和为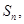
 (
( )
) 的首项
的首项 ,并判断
,并判断 的前n项和,求证:
的前n项和,求证:
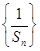 的前n项和,则Tn=( )
的前n项和,则Tn=( )