题目内容
【题目】已知圆
和圆
（
）.
（1）若圆
与圆
相外切，求
的值；
（2）若圆与
轴相切，求圆与圆的公共弦长.
【答案】（1）16（2）
【解析】
（1）首先根据圆
与圆
外切,根据两圆外切时,两圆圆心距离等于二者半径之和,即可求出参数
的值;
（2）根据圆与
轴相切,可求得圆的方程.通过作差法求出圆与圆的公共弦方程,利用圆圆心到公共弦的距离,根据几何关系求圆与圆的公共弦长.
（1）圆的圆心
半径
圆的方程化为标准方程得:
其圆心为
半径
由题意得
即
解得
（2）由上问可知
圆与轴相切时圆的半径
故
整理可得: 
圆与圆的公共弦长方程可由圆与圆作差求得:
即
整理公共弦长方程
:
圆的圆心到的距离为: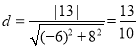
如图:
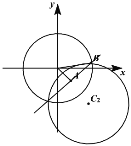
在
所以圆与圆的公共弦长:
综上所述圆与圆的公共弦长:.
练习册系列答案
相关题目
【题目】在平面直角坐标系xOy中，双曲线
：
经过点
，其中一条近线的方程为
，椭圆
：
与双曲线有相同的焦点
椭圆的左焦点，左顶点和上顶点分别为F，A，B，且点F到直线AB的距离为
．
求双曲线的方程；
求椭圆的方程．
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度，现在某市进行调查，随机调查了
人，他们年龄的频数分布及支持“生育二胎”人数如下表：
年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
支持“生 育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
（1）由以上统计数据填下面2乘2列联表，并问是否有99
的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异：
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
支持 | a= | c= | |
不支持 | b= | d= | |
合计 |
（2）若对年龄在
的被调查人中随机选取两人进行调查，恰好这两人都支持“生育二胎放开”的概率是多少？
参考数据：P