题目内容
 已知两定点M,N的坐标分别为(-6,0),(6,0),动点P与M,N的连线斜率之积为-
已知两定点M,N的坐标分别为(-6,0),(6,0),动点P与M,N的连线斜率之积为-| 4 | 9 |
分析:设出动点的坐标,根据动点P与M,N的连线斜率之积为-
,建立方程,即可求得动点P的轨迹方程
| 4 |
| 9 |
解答: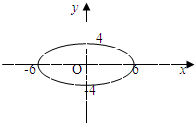 解:设动点P的坐标为(x,y),依题有kPM•kPN=-
解:设动点P的坐标为(x,y),依题有kPM•kPN=-
,…(3分)
又M(-6,0),N(6,0)
∴
•
=-
…(5分)
∴
+
=1
故所求动点P的轨迹方程为
+
=1…(8分)
依题作轨迹草图如图:
 解:设动点P的坐标为(x,y),依题有kPM•kPN=-
解:设动点P的坐标为(x,y),依题有kPM•kPN=-| 4 |
| 9 |
又M(-6,0),N(6,0)
∴
| y |
| x+6 |
| y |
| x-6 |
| 4 |
| 9 |
∴
| x2 |
| 36 |
| y2 |
| 16 |
故所求动点P的轨迹方程为
| x2 |
| 36 |
| y2 |
| 16 |
依题作轨迹草图如图:
点评:本题考查轨迹方程的求解,解题的关键是设点,建立方程,化简方程.

练习册系列答案
相关题目
 已知两定点M,N的坐标分别为(-6,0),(6,0),动点P与M,N的连线斜率之积为
已知两定点M,N的坐标分别为(-6,0),(6,0),动点P与M,N的连线斜率之积为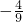 ,求动点P的轨迹方程,并画出轨迹草图.
,求动点P的轨迹方程,并画出轨迹草图. ,求动点P的轨迹方程,并画出轨迹草图.
,求动点P的轨迹方程,并画出轨迹草图.
 ,求动点P的轨迹方程,并画出轨迹草图.
,求动点P的轨迹方程,并画出轨迹草图.