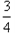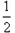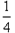题目内容
设椭圆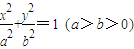 的中心、右焦点、右顶点依次分别为O、F、G,且直线
的中心、右焦点、右顶点依次分别为O、F、G,且直线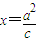 与x轴相交于点H,则
与x轴相交于点H,则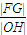 最大时椭圆的离心率为 .
最大时椭圆的离心率为 .
【答案】分析:确定F,G,O,H的坐标,求得距离,进而可求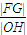 最大,从而可得此时离心率的值.
最大,从而可得此时离心率的值.
解答:解:由题设,H点的坐标为H(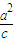 ,0),O(0,0),F(c,0),G(a,0)
,0),O(0,0),F(c,0),G(a,0)
∴|FG|=a-c,|OH|=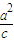
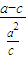 =
=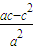 =e-e2=-(e2-e)=-(e-
=e-e2=-(e2-e)=-(e- )2+
)2+
∴当e= 时,
时,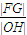 取得最大值,(
取得最大值,(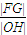 )max=
)max=
故答案为:
点评:本题考查椭圆的几何性质,考查配方法的运用,正确表示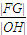 是关键.
是关键.
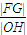 最大,从而可得此时离心率的值.
最大,从而可得此时离心率的值.解答:解:由题设,H点的坐标为H(
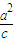 ,0),O(0,0),F(c,0),G(a,0)
,0),O(0,0),F(c,0),G(a,0)∴|FG|=a-c,|OH|=
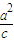
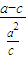 =
=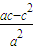 =e-e2=-(e2-e)=-(e-
=e-e2=-(e2-e)=-(e- )2+
)2+
∴当e=
 时,
时,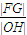 取得最大值,(
取得最大值,(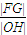 )max=
)max=
故答案为:

点评:本题考查椭圆的几何性质,考查配方法的运用,正确表示
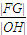 是关键.
是关键. 
练习册系列答案
相关题目
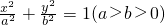 的中心、右焦点、右顶点依次分别为O、F、G,且直线
的中心、右焦点、右顶点依次分别为O、F、G,且直线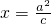 与x轴相交于点H,则
与x轴相交于点H,则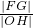 最大时椭圆的离心率为
最大时椭圆的离心率为


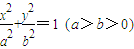 的中心、右焦点、右顶点依次分别为O、F、G,且直线
的中心、右焦点、右顶点依次分别为O、F、G,且直线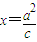 与x轴相交于点H,则
与x轴相交于点H,则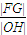 最大时椭圆的离心率为( )
最大时椭圆的离心率为( )


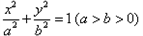 的中心、右焦点、右顶点依次分别为
的中心、右焦点、右顶点依次分别为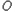 、
、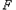 、
、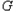 ,且直线
,且直线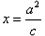 与
与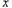 轴相交于点
轴相交于点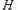 ,则
,则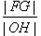 最大时椭圆的离心率为
最大时椭圆的离心率为