题目内容
已知函数f(x)=lnx+ax+b在x=3处的倾斜角为 ,则a的值为
,则a的值为
- A.

- B.

- C.

- D.
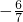
A
分析:求得导函数,利用函数f(x)=lnx+ax+b在x=3处的倾斜角为 ,可得f′(3)=-1,由此可求a的值.
,可得f′(3)=-1,由此可求a的值.
解答:求导函数可得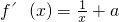
∵函数f(x)=lnx+ax+b在x=3处的倾斜角为 ,
,
∴f′(3)=-1
∴
∴a=
故选A.
点评:本题考查导数的几何意义,考查学生的计算能力,属于基础题.
分析:求得导函数,利用函数f(x)=lnx+ax+b在x=3处的倾斜角为
 ,可得f′(3)=-1,由此可求a的值.
,可得f′(3)=-1,由此可求a的值.解答:求导函数可得
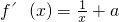
∵函数f(x)=lnx+ax+b在x=3处的倾斜角为
 ,
,∴f′(3)=-1
∴

∴a=

故选A.
点评:本题考查导数的几何意义,考查学生的计算能力,属于基础题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目