Question

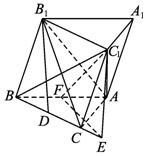
已知斜三棱柱ABC—A₁B₁C₁的底面是直角三角形,∠C=90°,侧棱与底面所成的角为α(0°＜α＜90°),点B₁在底面上的射影D落在BC上.

(1)求证:AC⊥平面BB₁C₁C.

(2)当α为何值时,AB₁⊥BC₁,且使D恰为BC中点?

(3)若α=arccos,且AC=BC=AA₁时,求二面角C₁—AB—C的大小.

Answer 1

(1)证明：∵B₁D⊥面ABC,AC⊥BC,

∴AC⊥BB₁.

∴AC⊥面BB₁C₁C.

(2)解：由(1)知AC⊥BC₁,∵BC₁⊥AB₁,

∴BC₁⊥面AB₁C.

∴BC₁⊥B₁C.

∴BCC₁B₁为菱形.∴BB₁=BC=2BD.

∴∠α=60°.

(3)解：设AC=a,过C₁作C₁E⊥BC于E,过E作EF⊥AB于F,

    则∠C₁FE为所求,C₁E=a,EF=×a=a,

∴∠C₁FE=45°.