题目内容
设正数数列![]() 的前
的前![]() 项和为
项和为![]() ,且对任意的
,且对任意的![]() ,
,![]() 是
是![]() 和
和![]() 的等差中项.(1)求数列
的等差中项.(1)求数列![]() 的通项公式;
的通项公式;
(2)在集合![]() ,
,![]() ,且
,且![]() 中,是否存在正整数
中,是否存在正整数![]() ,使得不等式
,使得不等式![]() 对一切满足
对一切满足![]() 的正整数
的正整数![]() 都成立?若存在,则这样的正整数
都成立?若存在,则这样的正整数![]() 共有多少个?并求出满足条件的最小正整数
共有多少个?并求出满足条件的最小正整数![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)请构造一个与数列![]() 有关的数列
有关的数列![]() ,使得
,使得![]() 存在,并求出这个极限值.
存在,并求出这个极限值.
(1)![]() (
(![]() ) (2)共有
) (2)共有![]() 个,
个,![]() 的最小值为
的最小值为![]()
(3)2
解析:
解:(1)由题意得,![]() ①,
①,
当![]() 时,
时,![]() ,解得
,解得![]() ,……(1分)
,……(1分)
当![]() 时,有
时,有![]() ②,
②,
①式减去②式得,![]()
于是,![]() ,
,![]() ,……(2分)
,……(2分)
因为![]() ,所以
,所以![]() ,
,
所以数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,……(3分)
的等差数列,……(3分)
所以![]() 的通项公式为
的通项公式为![]() (
(![]() ).……(4分)
).……(4分)
(2)设存在满足条件的正整数![]() ,则
,则![]() ,
,![]() ,
,
![]() ,……(6分)
,……(6分)
又![]()
![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,
,![]() ,…,
,…,![]()
![]() ,
,
所以![]() ,
,![]() ,…,
,…,![]() 均满足条件,
均满足条件,
它们组成首项为![]() ,公差为
,公差为![]() 的等差数列.……(8分)
的等差数列.……(8分)
设共有![]() 个满足条件的正整数,则
个满足条件的正整数,则![]() ,解得
,解得![]() .……(10分)
.……(10分)
所以,![]() 中满足条件的正整数
中满足条件的正整数![]() 存在,共有
存在,共有![]() 个,
个,![]() 的最小值为
的最小值为![]() .……(12分)
.……(12分)
(3)设![]() ,即
,即![]() ,……(15分),
,……(15分),
则![]()
![]() ,其极限存在,且
,其极限存在,且
![]() .……(18分)
.……(18分)
注:![]() (
(![]() 为非零常数),
为非零常数),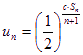 (
(![]() 为非零常数),
为非零常数),
![]() (
(![]() 为非零常数,
为非零常数,![]() )等都能使
)等都能使![]() 存在.
存在.
按学生给出的答案酌情给分,写出数列![]() 正确通项公式的得3分,求出极限再得3分.
正确通项公式的得3分,求出极限再得3分.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的各项均是正数,其前
的各项均是正数,其前 项和为
项和为 ,满足
,满足 ,其中
,其中 为正常数,且
为正常数,且
 ,数列
,数列 的前
的前 ,求证:
,求证:
 的前
的前 项和为
项和为 ,且
,且 ,
,
 ,
, ,
,
 的通项公式,并用数学归纳法证明
的通项公式,并用数学归纳法证明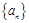 的各项均是正数,其前
的各项均是正数,其前 项和为
项和为 ,满足
,满足 ,其中
,其中 为正常数,且
为正常数,且
 ,数列
,数列 的前
的前 ,求证:
,求证: