题目内容
(本小题满分12分)已知 为坐标原点,向量
为坐标原点,向量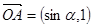 ,
,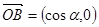 ,
,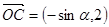 点
点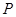 是直线
是直线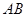 上一点,且
上一点,且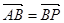 ;
;
(1)设函数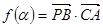 ,
, 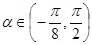 ,讨论
,讨论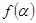 的单调性,并求其值域;
的单调性,并求其值域;
(2)若点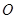 、
、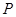 、
、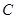 共线,求
共线,求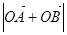 的值。
的值。
【答案】
(1)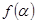 在
在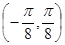 上单调递减,在
上单调递减,在 上单调递增,值域为
上单调递增,值域为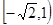 。(2)
。(2)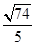 。
。
【解析】
试题分析:(1)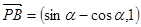 ,
,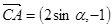 ,所以
,所以 .2分
.2分
所以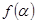 在
在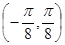 上单调递减,在
上单调递减,在 上单调递增……………… ………..4分
上单调递增……………… ………..4分
又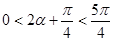 ,得到
,得到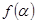 的值域为
的值域为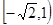 …………………………
………..6分
…………………………
………..6分
(2)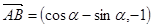 ,
,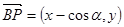 得到
得到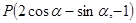 …..8分
…..8分
所以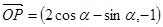 ,
,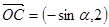 ,又因为
,又因为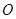 ,
,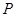 ,
,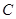 三点共线,
三点共线,
所以得到 ,所以
,所以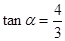 …………………………
………..10分
…………………………
………..10分
所以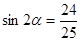 ,
,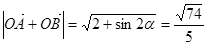 ………………
…… ………..12分
………………
…… ………..12分
考点:平面向量的数量积;三角函数的单调性及值域;向量共线的条件;向量的模的概念。
点评:本题以向量的方式来给出题设条件,来考查三角的有关知识,较为综合。同时本题对答题者公式掌握的熟练程度及知识点的灵活应用要求较高,是一道中档题.

练习册系列答案
相关题目