题目内容
m，n为异面直线，P为m，n外一点，则过点P与m，n都平行的平面有（ ）
分析：利用“m，n为异面直线，则存在唯一一对平面α∥β，使得m?α，n?β．”如图所示．及其线面平行的判定定理即可得出．
解答：解：∵m，n为异面直线，∴存在唯一一对平面α∥β，使得m?α，n?β．如图所示．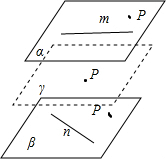
①当点P∈α或P∈β时，不存在过点P与m，n都平行的平面；
②当点P∉α且P∉β时，存在唯一过点P的平面γ，使得γ∥m，且γ∥n．
综上可知：过点P与m，n都平行的平面有0或1个．
故选B．
①当点P∈α或P∈β时，不存在过点P与m，n都平行的平面；
②当点P∉α且P∉β时，存在唯一过点P的平面γ，使得γ∥m，且γ∥n．
综上可知：过点P与m，n都平行的平面有0或1个．
故选B．
点评：熟练掌握结论“m，n为异面直线，∴存在唯一一对平面α∥β，使得m?α，n?β．”及其线面平行的判定定理是解题的关键．
练习册系列答案
相关题目
α，n
α，m，n是异面直线，那么n与α相交
α，n
α，n
α，m，n是异面直线，那么n与α相交
α，n
．有下列命题：①过m必能作平面α，使n⊥α；②过m必能作平面α，使n∥α；③过m能作平面γ，使n和γ成