题目内容
设椭圆 的焦点在
的焦点在 轴上
轴上
(Ⅰ)若椭圆 的焦距为1,求椭圆
的焦距为1,求椭圆 的方程;
的方程;
(Ⅱ)设 分别是椭圆的左、右焦点,
分别是椭圆的左、右焦点, 为椭圆
为椭圆 上第一象限内的点,直线
上第一象限内的点,直线 交
交 轴与点
轴与点 ,并且
,并且 ,证明:当
,证明:当 变化时,点
变化时,点 在某定直线上.
在某定直线上.
【答案】
(Ⅰ) (Ⅱ)见解析
(Ⅱ)见解析
【解析】(1)由题意 ,得
,得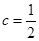 ,
,
而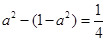 ,所以
,所以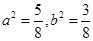
所以椭圆的标准方程为

(2)设 ,
,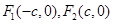
直线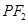 的直线方程为
的直线方程为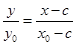 ,当
,当 时,
时,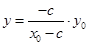 ,
,
故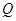 点坐标
点坐标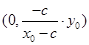 ,
,
由题意
得
即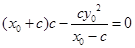
解得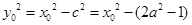
又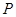 点在曲线上,
点在曲线上, ,解得
,解得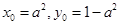
则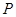 点在定直线
点在定直线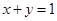 .
.
根据题意确定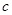 的大小,以及
的大小,以及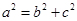 ,可以很快求出椭圆
,可以很快求出椭圆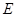 的方程,但容易弄混长轴长(
的方程,但容易弄混长轴长(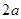 )、短轴长(
)、短轴长( )和焦距(
)和焦距(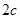 )的概念,简单题;第(2)属于定直线问题,对于定直线问题,需要根据题意确定动点的坐标,再确定动点横纵坐标的关系,其实是变向的考查求动点
)的概念,简单题;第(2)属于定直线问题,对于定直线问题,需要根据题意确定动点的坐标,再确定动点横纵坐标的关系,其实是变向的考查求动点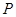 的轨迹方程问题,本题可以设出
的轨迹方程问题,本题可以设出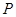 点的坐标,根据垂直关系,利用向量或斜率求出
点的坐标,根据垂直关系,利用向量或斜率求出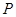 的坐标关系式,再利用
的坐标关系式,再利用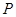 在圆锥曲线上,即可求出
在圆锥曲线上,即可求出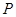 点坐标,继而能够确定
点坐标,继而能够确定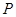 点在定直线上,属于中档题.
点在定直线上,属于中档题.
【考点定位】考查椭圆的标准方程及其几何性质,直线与直线,直线与椭圆的位置关系.

练习册系列答案
相关题目
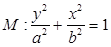 (
(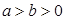 )经过点
)经过点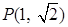 ,其离心率与双曲线
,其离心率与双曲线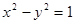 的离心率互为倒数.
的离心率互为倒数.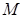 的方程;(注意椭圆的焦点在
的方程;(注意椭圆的焦点在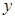 轴上哦!)
轴上哦!)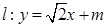 交椭圆
交椭圆 两点,求
两点,求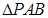 面积的最大值.
面积的最大值.
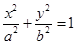 的焦点在
的焦点在 轴上,
轴上,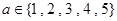 ,
,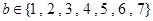 ,则这样的椭圆个数共有
( )
,则这样的椭圆个数共有
( )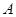 、
、
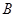 、
、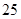
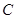 、
、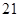
 、
、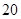
 的焦点在
的焦点在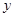 轴上,
轴上, ,
,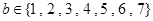 ,则这样的椭圆个数共有 ( )
,则这样的椭圆个数共有 ( )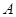 、
、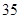
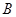 、
、
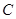 、
、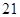
 、
、