题目内容
如图，已知四边形OABC中，M为BC中点，N为AC中点，P为OA中点，Q为OB中点，若AB=OC.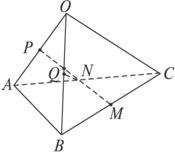
求证:PM⊥QN.
分析：欲证PM⊥QN,只需证明
·
=0.
证明：设
=a,
=b,
=c.
∵
(b+c),
(a+c),
∴
=-
a+
(b+c)=
(b+c-a),
=-
b+
(a+c)=
(a+c-b),
∴
=
［c-(a-b)］［c+(a-b)］
=
［c2-(a-b)2］=
(|
|2-|
2).
∵|
|=|
|,∴
·
=0.
∴
⊥
,∴PM⊥QN.
点拨：要证明两线垂直，需转化为两线对应的向量垂直，进一步转化为证明两向量的数量积为零，此题关键是正确选取基底，并用基向量表示PM，QN.
练习册系列答案
相关题目
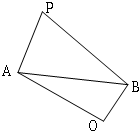如图，已知四边形PAOB中，PA⊥OA，PB⊥OB．且PA=5，PB=8，AB=7
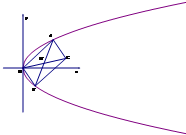如图，已知抛物线P：y2=x，直线AB与抛物线P交于A，B两点，OA⊥OB，
如图，已知空间四边形OABC，其对角线为OB、AC，M、N分别是对边OA、BC的中点，点G在线段MN上，且