题目内容
(本小题满分12分)
△A BC中,内角A、B、C的对边分别为a、b、c
BC中,内角A、B、C的对边分别为a、b、c
(I)若△ABC面积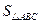 =
=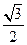 ,c=2,A=60°,求a,b的值
,c=2,A=60°,求a,b的值
(Ⅱ)若a=c·cosB,且b=c·sinA,试判断△ABC的形状
△A
 BC中,内角A、B、C的对边分别为a、b、c
BC中,内角A、B、C的对边分别为a、b、c(I)若△ABC面积
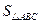 =
=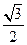 ,c=2,A=60°,求a,b的值
,c=2,A=60°,求a,b的值(Ⅱ)若a=c·cosB,且b=c·sinA,试判断△ABC的形状
解:(Ⅰ)
 ,
,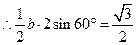 ,得
,得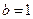
由余弦定理得:
 ,
,得
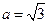 故
故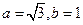 ………………6分
………………6分(Ⅱ)由余弦定理得:
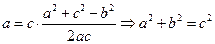 ,所以
,所以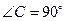
在
 中,
中, ,所以
,所以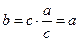
故△

 是等腰直角三角形;
是等腰直角三角形; 
 ………………12分
………………12分略

练习册系列答案
相关题目
 中,
中, ,
, ,
, ,则
,则 ( )
( )



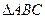 中,
中,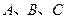 的对边分别为
的对边分别为
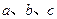 ,且
,且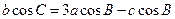 .
. 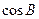 的值;
的值;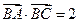 ,
,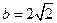 ,求
,求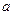 和
和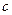 .
. 相距9海里的C处有一艘走私船,正沿南偏东75
相距9海里的C处有一艘走私船,正沿南偏东75
 中, a,b,c分别是A、B、C的对边,且
中, a,b,c分别是A、B、C的对边,且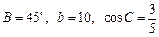 .
. 中,
中,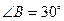 ,
,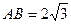 ,
,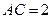 ,求
,求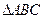 的面积是30,
的面积是30,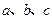 分别是三内角
分别是三内角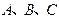 的对边,且
的对边,且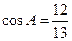 .
.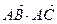 ; (2)若
; (2)若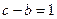 ,求
,求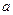 的值。
的值。