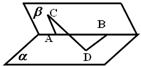
题目内容
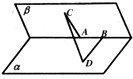如图，60°的二面角的棱上有A、B两点，线段AC、BD分别在这个二面角的两个半平面内，且都垂直于AB，已知AB=4，AC=6，BD=8，则CD的长为（ ）分析：由已知可得
=
+
+
，利用数量积的性质即可得出．
| CD |
| CA |
| AB |
| BD |
解答：解：∵CA⊥AB，BD⊥AB，∴
=
•
=0，
∵＜
，
＞=60°，∴＜
，
＞=120°．
∵
=
+
+
，
∴
2=
2+
2+
2+2
•
+2
•
+2
•
=62+42+82+0+2×6×8×cos120°+0
=68．
∴|
|=2
．
故选A．
| CA• |
| AB |
| BD |
| AB |
∵＜
| AC |
| BD |
| CA |
| BD |
∵
| CD |
| CA |
| AB |
| BD |
∴
| CD |
| CA |
| AB |
| BD |
| CA |
| AB |
| CA |
| BD |
| AB |
| BD |
=62+42+82+0+2×6×8×cos120°+0
=68．
∴|
| CD |
| 17 |
故选A．
点评：熟练掌握向量的运算和数量积运算是解题的关键．
练习册系列答案
相关题目
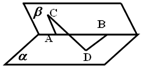如图，60°的二面角的棱上有A、B两点，直线AC、BD分别在这个二面角的两个半平面内，且都垂直AB，已知AB=4，AC=6，BD=8，求CD的长．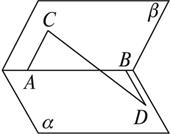
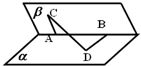β,BD
α,AC⊥AB于A,BD⊥AB于B,且AC=AB=BD=1,则CD的长为… ( )
C.2 D.
如图，60°的二面角的棱上有A、B两点，直线AC、BD分别在这个二面角的两个半平面内，且都垂直AB，已知AB=4，AC=6，BD=8，求CD的长．