题目内容
某厂生产产品x件的总成本c(x)=
x3(万元),已知产品单价P(万元) 与产品件数x满足:P2=
,生产1件这样的产品单价为16万元.
(1)设产量为x件时,总利润为L(x)(万元),求L(x)的解析式;
(2)产量x定为多少件时总利润L(x)(万元)最大?
| 1 |
| 12 |
| k |
| x |
(1)设产量为x件时,总利润为L(x)(万元),求L(x)的解析式;
(2)产量x定为多少件时总利润L(x)(万元)最大?
分析:(1)利用一件产品的单价可得得出k,进而得出P与x的关系,用毛利润减去总成本即可得出总利润;
(2)利用导数即可得出极大值,进而得到最大值.
(2)利用导数即可得出极大值,进而得到最大值.
解答:解:(1)由题意有162=
,解得k=256,
∴P=
=
,
∴总利润L(x)=x•
-
=-
+16
(x>0);
(2)由(1)得L′(x)=-
x2+
,令L′(x)=0⇒
=
x2,
解得x=4,则x=4,所以当产量定为4时,总利润最大.
答:产量x定为4件时总利润L(x)最大.
| k |
| 1 |
∴P=
|
| 16 | ||
|
∴总利润L(x)=x•
| 16 | ||
|
| x3 |
| 12 |
| x3 |
| 12 |
| x |
(2)由(1)得L′(x)=-
| 1 |
| 4 |
| 8 | ||
|
| 8 | ||
|
| 1 |
| 4 |
解得x=4,则x=4,所以当产量定为4时,总利润最大.
答:产量x定为4件时总利润L(x)最大.
点评:熟练掌握利润与成本的关系、利用导数研究函数的单调性极值与最值等是解题的关键.

练习册系列答案
相关题目
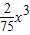 (万元),已知产品单价P(万元)与产品件数x满足:P2=
(万元),已知产品单价P(万元)与产品件数x满足:P2=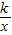 ,生产100件这样的产品单价为50万元,产量定为多少件时总利润最大?
,生产100件这样的产品单价为50万元,产量定为多少件时总利润最大?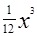 (万元),已知产品单价P(万元) 与产品件数x满足:
(万元),已知产品单价P(万元) 与产品件数x满足: ,生产1件这样的产品单价为16万元.
,生产1件这样的产品单价为16万元.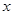 件时,总利润为
件时,总利润为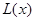 (万元),求
(万元),求