题目内容
已知函数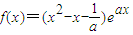 (a>0且a为常数).
(a>0且a为常数).(Ⅰ)当a=2时,求函数f(x)的单调区间;
(Ⅱ)若不等式
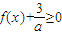 对x∈[-
对x∈[-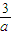 ,+∞)恒成立,求a的取值范围.
,+∞)恒成立,求a的取值范围.
【答案】分析:(I)由题意把a代入解析式使解析式具体,在对函数f(x)利用导数法则求其导函数,令导函数大于0,求出函数的增区间,令导函数小于0求出函数的减区间;
(II)由题意,此问题属于函数的恒成立问题,转化为函数在定义域内求最值,在令最小值还大于等于0即可.
解答:解:对函数f(x)求导得:f′(x)=eax(ax+2)(x-1)
(Ⅰ)当a=2时,f′(x)=e2x(2x+2)(x-1)
令f′(x)>0解得x>1或x<-1;
令f′(x)<0解得-1<x<1;
所以,f(x)单调增区间为(-∞,-1),(1,+∞);
f(x)单调减区间为(-1,1)
(Ⅱ)令f′(x)=0,即(ax+2)(x-1)=0,
解得 或x=1
或x=1
由a>0时,得:当x∈(-∞,- )时,f′(x)>0,函数f(x)此区间单调递增;
)时,f′(x)>0,函数f(x)此区间单调递增;
当 时,f′(x)<0,函数f(x)在此区间单调递减;
时,f′(x)<0,函数f(x)在此区间单调递减;
当x∈(1,+∞)时,f′(x)>0,函数f(x)在此区间单调递增,

∵f(- )>0,f(1)<0,所以,函数在x=1时取得最小值
)>0,f(1)<0,所以,函数在x=1时取得最小值
所以,当x∈R时, ,
,
由题意,不等式 对x∈R恒成立,
对x∈R恒成立,
所以得 ,解得0<a≤ln3.
,解得0<a≤ln3.
点评:(I)此题考查了利用导函数求其定义域下的单调区间;
(II)此题考查了函数在x∈R下恒成立为题可以等价的转化为函数在定义域下最小值还大于等于0成立,此处等价转化的思想在高考中常用.
(II)由题意,此问题属于函数的恒成立问题,转化为函数在定义域内求最值,在令最小值还大于等于0即可.
解答:解:对函数f(x)求导得:f′(x)=eax(ax+2)(x-1)
(Ⅰ)当a=2时,f′(x)=e2x(2x+2)(x-1)
令f′(x)>0解得x>1或x<-1;
令f′(x)<0解得-1<x<1;
所以,f(x)单调增区间为(-∞,-1),(1,+∞);
f(x)单调减区间为(-1,1)
(Ⅱ)令f′(x)=0,即(ax+2)(x-1)=0,
解得
 或x=1
或x=1由a>0时,得:当x∈(-∞,-
 )时,f′(x)>0,函数f(x)此区间单调递增;
)时,f′(x)>0,函数f(x)此区间单调递增;当
 时,f′(x)<0,函数f(x)在此区间单调递减;
时,f′(x)<0,函数f(x)在此区间单调递减;当x∈(1,+∞)时,f′(x)>0,函数f(x)在此区间单调递增,

∵f(-
 )>0,f(1)<0,所以,函数在x=1时取得最小值
)>0,f(1)<0,所以,函数在x=1时取得最小值
所以,当x∈R时,
 ,
,由题意,不等式
 对x∈R恒成立,
对x∈R恒成立,所以得
 ,解得0<a≤ln3.
,解得0<a≤ln3.点评:(I)此题考查了利用导函数求其定义域下的单调区间;
(II)此题考查了函数在x∈R下恒成立为题可以等价的转化为函数在定义域下最小值还大于等于0成立,此处等价转化的思想在高考中常用.

练习册系列答案
相关题目
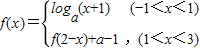 (a>0且a≠1),若x1≠x2,且f(x1)=f(x2),则x1+x2的值( )
(a>0且a≠1),若x1≠x2,且f(x1)=f(x2),则x1+x2的值( )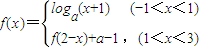 (a>0且a≠1),若x1≠x2,且f(x1)=f(x2),则x1+x2的值( )
(a>0且a≠1),若x1≠x2,且f(x1)=f(x2),则x1+x2的值( ) (a>0且a为常数).
(a>0且a为常数). 对x∈[-
对x∈[- ,+∞)恒成立,求a的取值范围.
,+∞)恒成立,求a的取值范围. 其中a>0,且a≠1,
其中a>0,且a≠1, 的定义域;
的定义域; ;
; 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. =loga
=loga (a>0且a≠1)是奇函数
(a>0且a≠1)是奇函数 ,(
,(